
A magnetic field due to a long straight wire carrying a current
A.
B.
C.
D.
Answer
484.2k+ views
Hint: Apply Biot- savart’s law by considering an elementary length on the finite straight wire. For the long or infinite length of the straight wire or any conductor, the perpendicular distance from the wire is at the center of the wire that
Complete step by step solution:
Let us consider an straight wire through which current
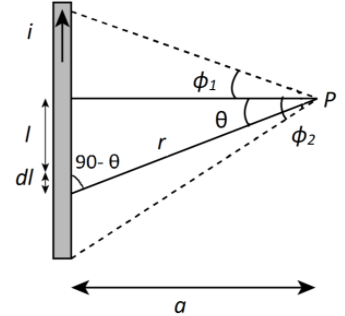
Now let
Now we apply Bio- savart’s law, the magnetic field due to the current element
From the triangle formed by
And
Now differentiate above equation with respect to
Now we substitute the values of
Now we integrate from
After further simplifying, we get,
It is given in the question that the straight wire is long that is infinite, in this the point
Now substitute
Since
Thus, the magnetic field (
So, the correct answer is “Option A”.
Note:
Be careful while answering because the formula for finite straight wire and infinite straight is completely different.
When wire has finite length:
When wire has infinite length,
When wire has infinite length and point
Complete step by step solution:
Let us consider an straight wire through which current

Now let
Now we apply Bio- savart’s law, the magnetic field due to the current element
From the triangle formed by
And
Now differentiate above equation with respect to
Now we substitute the values of
Now we integrate from
After further simplifying, we get,
It is given in the question that the straight wire is long that is infinite, in this the point
Now substitute
Since
Thus, the magnetic field (
So, the correct answer is “Option A”.
Note:
Be careful while answering because the formula for finite straight wire and infinite straight is completely different.
When wire has finite length:
When wire has infinite length,
When wire has infinite length and point
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




