Question

A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at the most 12 hours a day?
$
  {\text{A}}{\text{. 1}} \\
  {\text{B}}{\text{. 2}} \\
  {\text{C}}{\text{. 3}} \\
  {\text{D}}{\text{. 4}} \\
 $

Answer 1

Hint: Here, we will proceed by making the linear inequalities according to the problem statement and then obtaining the feasible solution which will satisfy all the linear inequalities and then finding the value of the function (which needs to be maximized) corresponding to all the corner points of the feasible point.

Complete step-by-step answer:

Let x be the number of packages of nuts produced each day and y be the number of packages of bolts produced each day.
According to the problem statement,
In order to produce 1 package of nuts, 1 hour of work on machine A and 3 hours of work on machine B is required.
In order to produce 1 package of bolts, 3 hours of work on machine A and 1 hour of work on machine B is required.
Also, machines A and B operate for a maximum of 12 hours a day.
$
  x + 3y \leqslant 12{\text{ }} \to {\text{(1)}} \\
  3x + y \leqslant 12{\text{ }} \to {\text{(2)}} \\
 $
Since, the number of packages can never be negative.
$
  x \geqslant 0{\text{ }} \to {\text{(3)}} \\
  y \geqslant 0{\text{ }} \to {\text{(4)}} \\
 $
Profit function is given by
\[z = 17.5x + 7y{\text{ }} \to {\text{(5)}}\]
Here, we need to maximize the profit function i.e., z
Consider the straight line $x + 3y = 12{\text{ }} \to {\text{(6)}}$
Put x = 0 in equation (6), we get
$
   \Rightarrow 0 + 3y = 12 \\
   \Rightarrow y = 4 \\
 $
Put y = 0 in equation (6), we get
$
   \Rightarrow x + \left( {3 \times 0} \right) = 12 \\
   \Rightarrow x = 12 \\
 $
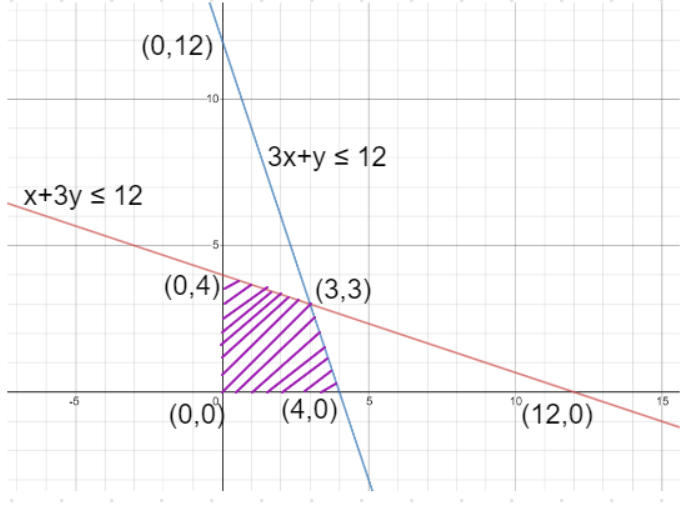
So, the passing points of the straight line given by equation (6) are (0,4) and (12,0).
Consider the straight line $3x + y = 12{\text{ }} \to {\text{(7)}}$
Put x = 0 in equation (7), we get
\[
   \Rightarrow \left( {3 \times 0} \right) + y = 12 \\
   \Rightarrow y = 12 \\
 \]
Put y = 0 in equation (7), we get
$
   \Rightarrow 3x + 0 = 12 \\
   \Rightarrow x = 4 \\
 $
So, the passing points of the straight line given by equation (7) are (0,12) and (4,0).
Let us plot both these straight lines given by equations (6) and (7) which are obtained by considering just the equality of the linear inequalities (1) and (2).
Since, the origin O(0,0) satisfies both the linear inequalities given by (1) and (2).
The linear inequalities given by (3) and (4) refer that only the first quadrant is feasible for the solution.
So, the feasible region which satisfies all the four linear inequalities is coloured violet as shown in the figure.
Equation (6) can be rewritten as
$ \Rightarrow x = 12 - 3y$
Put the value of x from the above equation in equation (7), we get
$
   \Rightarrow 3\left( {12 - 3y} \right) + y = 12 \\
   \Rightarrow 36 - 9y + y = 12 \\
   \Rightarrow 8y = 24 \\
   \Rightarrow y = 3 \\
 $
Put y = 3 in the equation $x = 12 - 3y$, we have
$
   \Rightarrow x = 12 - \left( {3 \times 3} \right) \\
   \Rightarrow x = 12 - 9 \\
   \Rightarrow x = 3 \\
 $
The point where both the straight lines given by equations (6) and (7) will meet is (3,3)
Corner points of the feasible region (coloured at violet) are (0,0), (4,0), (3,3) and (0,4).
For point (0,0), \[
  z = 17.5x + 7y \\
   \Rightarrow z = \left( {17.5 \times 0} \right) + \left( {7 \times 0} \right) \\
   \Rightarrow z = 0 \\
 \]
For point (4,0), \[
  z = 17.5x + 7y \\
   \Rightarrow z = \left( {17.5 \times 4} \right) + \left( {7 \times 0} \right) \\
   \Rightarrow z = 70 \\
 \]
For point (3,3), \[
  z = 17.5x + 7y \\
   \Rightarrow z = \left( {17.5 \times 3} \right) + \left( {7 \times 3} \right) \\
   \Rightarrow z = 73.5 \\
 \]
For point (0,4), \[
  z = 17.5x + 7y \\
   \Rightarrow z = \left( {17.5 \times 0} \right) + \left( {7 \times 4} \right) \\
   \Rightarrow z = 0 + 28 \\
   \Rightarrow z = 28 \\
 \]
Clearly, the maximum value of the profit function z is Rs 73.5.
Therefore, the number of packages of nuts produced each day is 3 and the number of packages of bolts produced each day is 3 i.e., 3 packages each.
Hence, option C is correct.

Note: In this particular problem, if we will put x = 0 and y = 0 in the linear inequalities $x + 3y \leqslant 12$ and $3x + y \leqslant 12$, we will get $0 \leqslant 12$ which is true. This means that origin (0,0) satisfies both the linear inequalities. In order to find the point corresponding to which the maximum or minimum value of the function occurs, we will find all the extremes points (i.e., corner points) of the feasible region.