Question

State and prove converse of BPT (Basic Proportionality Theorem).

Answer 1

Hint: Suppose another line that is parallel to the side (which is not getting intersected with the line which divides two sides in the same ratio) other than the line which divides the sides in the same ratio and basic proportionality theorem can be given as: If a line is drawn parallel to one side of a triangle and intersecting other two sides, then line divides the intersecting sides in the same ratio. Use this property to solve the given problem.

Complete step by step answer:
BPT stands for basic proportionality theorem. It states that if a line is drawn parallel to one side of a triangle intersecting the other two sides in distinct points, then the other two sides are divided in the same ratio. So, if we draw a triangle ABC as

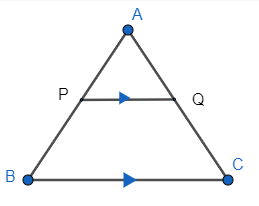
Where $PQ||BC$ , so according to basic proportionality theorem as stated above we have,
$\dfrac{AP}{PB}=\dfrac{AQ}{CQ}.................\left( i \right)$

Hence, converse of basic proportionality theorem can be stated as if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle. So, let us suppose a $\Delta ABC$ such that DE is a line which divides the two sides in the same ratio and draw a line DE’ which is parallel to the other side BC as shown in the diagram below:

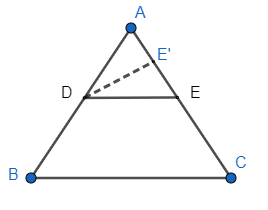
Here, DE is a line which divides AB and AC in the same ratio and DE is parallel to side BC. So, we have$\begin{align}
  & \dfrac{AD}{DB}=\dfrac{AE}{EC}....................\left( ii \right) \\
 & D{{E}^{'}}||BC\left( \text{construction} \right)...........\left( iii \right) \\
\end{align}$
In $\Delta ABC$ , we know $D{{E}^{'}}||BC$ by our own construction. It means we can use basic proportionality theorem as DE’ is parallel to side BC and hence will divide the sides AD and DB and AE’ and AC in the same ratio (as BPT explained initially) from the equation (i). So, we can write equation as
$\dfrac{AD}{DB}=\dfrac{A{{E}^{'}}}{{{E}^{'}}C}......................\left( iv \right)$
Now, from equation (ii) and (iv) we get
$\dfrac{AE}{EC}=\dfrac{A{{E}^{'}}}{{{E}^{'}}C}$
Add 1 to the both sides of the above equation, we get
$\begin{align}
  & \dfrac{AE}{EC}+1=\dfrac{A{{E}^{'}}}{{{E}^{'}}C}+1 \\
 & \Rightarrow \dfrac{AE+EC}{EC}=\dfrac{AE'+{{E}^{'}}C}{{{E}^{'}}C} \\
\end{align}$
Now, we can observe that the sum of AE and EC is the side AC and sum of $A{{E}^{'}},{{E}^{'}}C$ side is AC as well. So, we get
$\begin{align}
  & \dfrac{AC}{EC}=\dfrac{AC}{{{E}^{'}}C} \\
 & \Rightarrow \dfrac{1}{EC}=\dfrac{1}{{{E}^{'}}C} \\
\end{align}$
Reverse fractions from both sides of the equation, we get
$EC={{E}^{'}}C$
Now, it can be only possible if E and ${{E}^{'}}$ will lie at one point only i.e. both should coincide. Hence, E and ${{E}^{'}}$ are the same points. It means line DE and $D{{E}^{'}}$ are the same and lie on one another (coincide). So, DE will be parallel to side BC as well as $D{{E}^{'}}$ was parallel to the side BC (by construction). Hence, the converse of BPT is proved.

Note: Another approach for solving this property would be that we can prove the triangles similar to each other and hence use the property of similar triangles that angles of similar triangles are same.

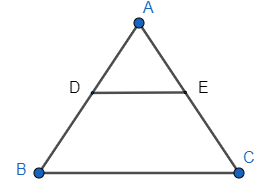
So, let DE divide two sides in the same ratio. It means we have
$\dfrac{AD}{DB}=\dfrac{AE}{EC}$
Now, reverse the fraction of above equation we get
$\dfrac{DB}{AD}=\dfrac{EC}{AE}$
Add 1 to both sides we get
$\begin{align}
  & \dfrac{DB}{AD}+1=\dfrac{EC}{AE}+1 \\
 & \dfrac{DB+AD}{AD}=\dfrac{EC+AE}{AE} \\
 & \dfrac{AB}{AD}=\dfrac{AC}{AE} \\
 & \Rightarrow \dfrac{AD}{AB}=\dfrac{AE}{AC} \\
\end{align}$
Now, in $\Delta ADE,ABC$ we have common
$\begin{align}
  & \angle A=\angle A \\
 & \dfrac{AD}{AB}=\dfrac{AE}{AC} \\
\end{align}$
It means $\Delta ADE,ABC$ are similar to each other. It means corresponding angles of them should be equal. So, we get
$\begin{align}
  & \angle ADE=\angle ABC, \\
 & \angle AED=\angle ACB \\
\end{align}$
As we know $\angle ADE,\angle ABC$ are similar to $\angle AED,\angle ACB$ can only be equal if $DE||BC$ as both are the corresponding angles through a transversal by two parallel lines. So, it can be another approach.