Question

A manufacturer produces nuts and bolts. It takes 1 hours of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7 per package of bolts. How many packages of each should be produced each day so as to maximize his profits if he operates his machines for at most 12 hours a day? From the above as a linear programming problem and solve it graphically.

Answer 1

HINT:In linear programming, we try to get a required region that is enclosed by the constraints that we form by reading the question and then try to maximize a statement that we only form by reading the question itself.It is a mathematical tool to improve the production by industrial units and to extract more profits.

Complete step by step answer:
Let the number of packets of nuts produced be x and the number of packets of bolts produced be y.
We have to maximize x & y if the factory works at capacity of 12hours per day.
Clearly,
\[x\ge 0\ and\ y\ge 0\]
(This is because the number of nuts and bolts produced cannot be negative)

As mentioned in the question, we have only 12 hours of machine, we will use the following constraints:-
\[x+3y\le 12~~\ldots \left( a \right)\]
\[3x+y\le 12~~\ldots \left( b \right)\]
Here, equation (a) is for production of nuts and equation (b) is for production of bolts.
The profit on the production of nuts is Rs.17.5 per packet and the profit on the production of bolts is Rs. 7 per packet.
We need to maximize 17.5x+7y.
Hence, z=17.5x+7y
(This is the maximizing statement)
We can see that the applicable region is bounded and in the first quadrant.
On solving the equations, x+3y=12 and 3x+y=12, we get

\[\begin{align}
  & x=3~ \\
 & y=3 \\
\end{align}\]
Therefore, required points are points are (0,0), (0,4), (3,3) and (4,4) as these are the corner points.

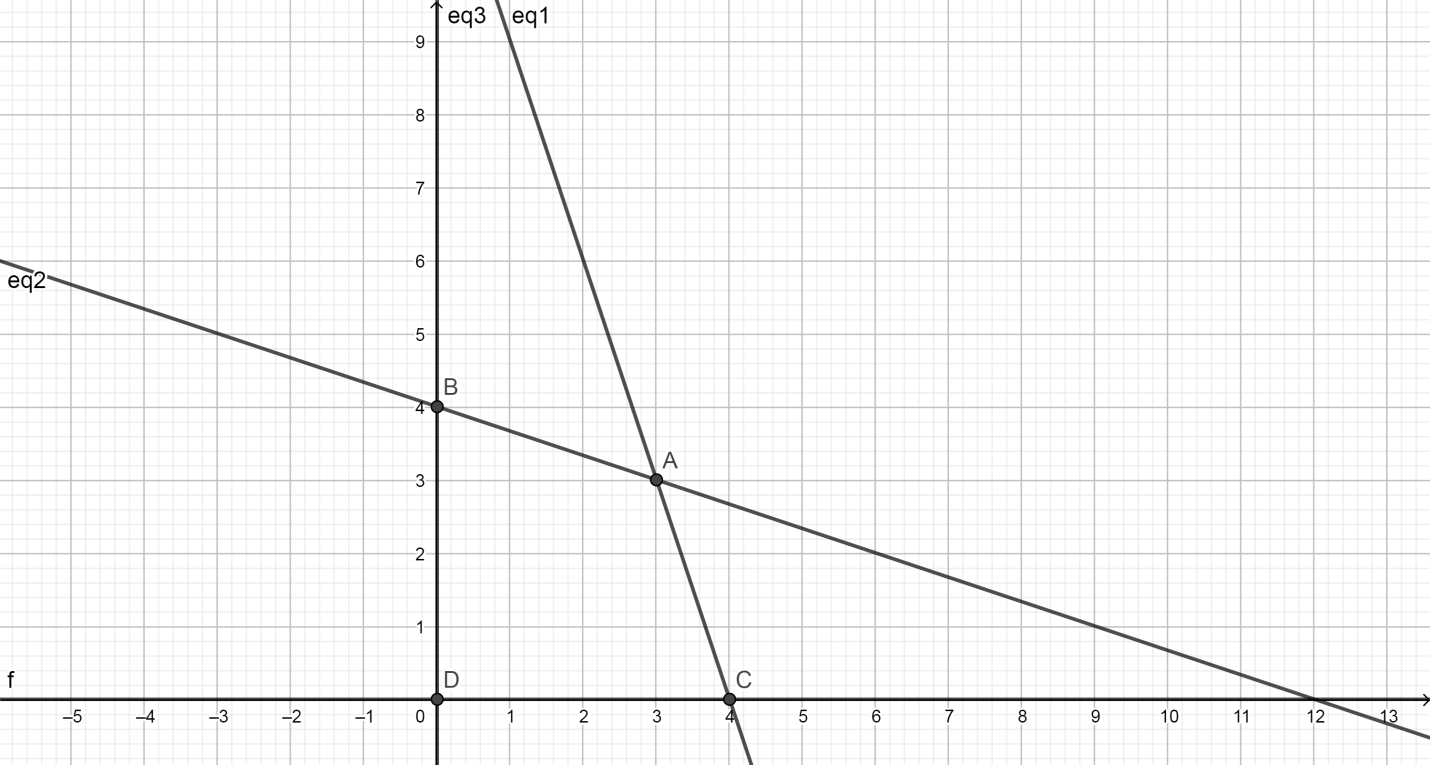
Hence, on plugging in these points in the maximizing statement, we get that
The maximum profit or the maximum value of z =73.5 which is when 3 packets each of nuts & bolts are produced.

NOTE:The students can make a mistake if he or she is not aware of the information about linear programming that in linear programming, we try to get a required region that is enclosed by the constraints that we form by reading the question and then try to maximize a statement that we only form by reading the question itself.