Question

A median of a triangle divides it into two triangles of equal areas. Verify this result for $\vartriangle ABC$ whose vertices are A (4, -6), B (3, -2) and C (5, 2).

Answer 1

Hint: Here we go through by first drawing the diagram for better understanding and then first finding out the coordinates of the median and then finding out the area of both triangles if they are equal the results are verified.

Complete step-by-step answer:

Here in the question the given triangle is $\vartriangle ABC$ . We draw a median AD to the side BC of the triangle and we know that the median bisect the sides into two equal parts.

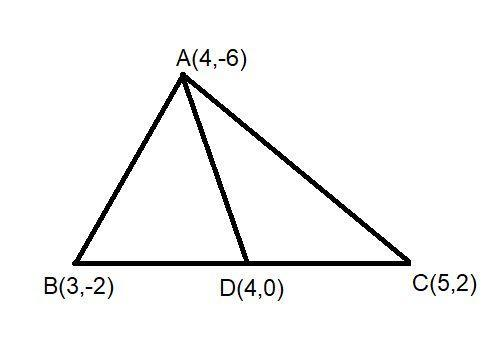
And in the question the coordinates of points are given that are A (4, -6), B (3, -2) and C (5, 2).
And now for finding the coordinates of D we will apply the midpoint rule because D is the midpoint of line BC.
So we can say $D\left( {\dfrac{{3 + 5}}{2},\dfrac{{ - 2 + 2}}{2}} \right) \equiv D\left( {4,0} \right)$
And now for proving the areas of two triangles ABD and ADC are equal we will find out their area separately by the formula ${\text{area of }}\vartriangle = \left| {\dfrac{1}{2}\left[ {{x_1}\left( {{y_2} - {y_3}} \right) + {x_2}\left( {{y_3} - {y_1}} \right) + {x_3}\left( {{y_1} - {y_3}} \right)} \right]} \right|$ we us this formula when the three coordinates of triangle are given as $({x_1},{y_1})$, $({x_2},{y_2})$ and $({x_3},{y_3})$.
Now for finding the area of $\vartriangle ABD$ the coordinates are A (4, -6), B (3, -2) and D (4, 0).
Put these coordinates in the formula we get,
$
  {\text{area of }}\vartriangle = \left| {\dfrac{1}{2}\left[ {4\left( { - 2 - 0} \right) + 3\left( {0 - ( - 6)} \right) + 4\left( { - 6 - 0} \right)} \right]} \right| \\
   = \left| {\dfrac{1}{2}\left[ { - 8 + 18 - 24} \right]} \right| \\
   = \left| { - 7} \right| \\
   = 7 \\
 $
Here we will out -7 from mode it will become 7 by the property of mode.
Now we will find the area of $\vartriangle ADC$ the coordinates are A (4, -6), C (5, 2) and D (4, 0).
Put these coordinates in the formula we get,
$
  {\text{area of }}\vartriangle = \left| {\dfrac{1}{2}\left[ {4\left( {2 - 0} \right) + 5\left( {0 - ( - 6)} \right) + 4\left( { - 6 - 0} \right)} \right]} \right| \\
   = \left| {\dfrac{1}{2}\left[ {8 + 30 - 24} \right]} \right| \\
   = \left| 7 \right| \\
   = 7 \\
 $
Here we clearly see that the area of $\vartriangle ABD$ and $\vartriangle ADC$ are equal i.e. 7sq.unit.
Hence we can say that a median of a triangle divides it into two triangles of equal areas.

Note: Whenever we face such a type of question the key concept for solving the question is to first draw the diagram as per the statements of the question then point out the coordinates. And then find out the value of coordinates that is not given in the question. After that by applying the formula of triangle when three coordinates are given we will be able to find their area by this we will verify our question easily.