
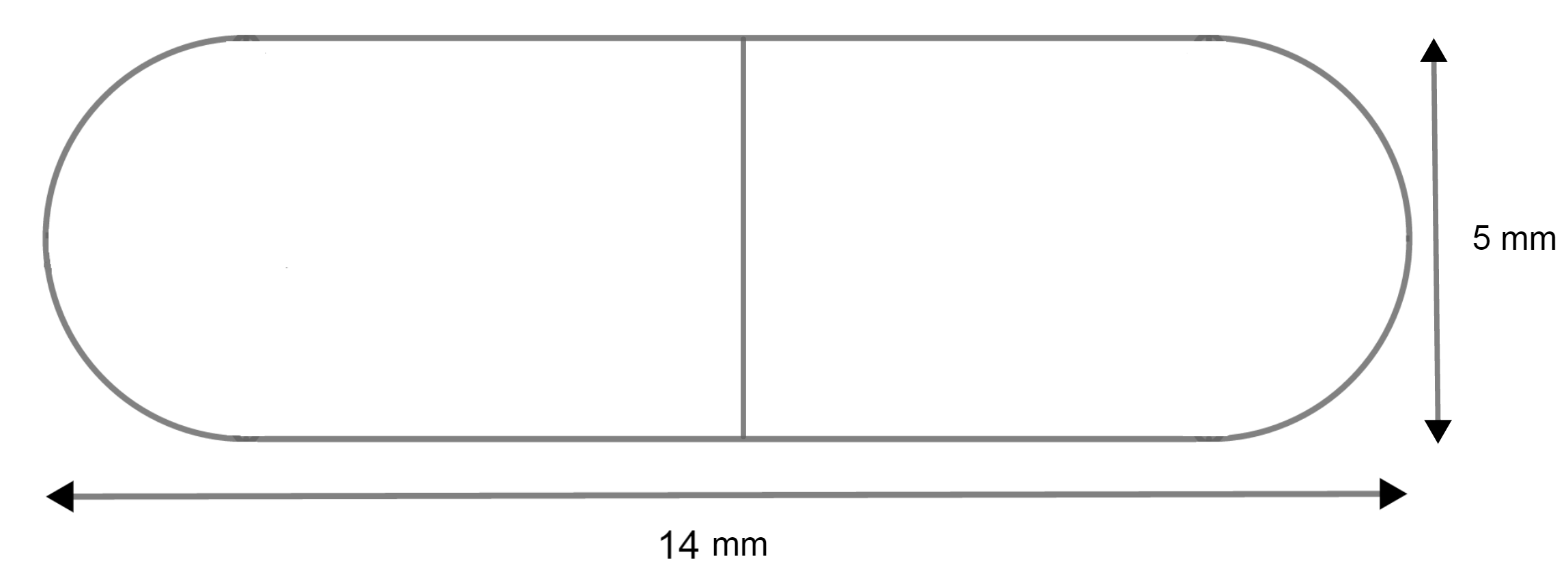
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14mm and the diameter of the capsule is 5mm. Find its surface area.

Answer
418.4k+ views
Hint: At first, try to find out the curved surface area of each of the hemispheres and the cylinder. The formula for calculating curved surface area of cylinder is \[2\pi rh\] and that of hemisphere is \[2\pi {{r}^{2}}\] where, r is the radius of the base and h is the height of cylinder.
Complete step-by-step answer:
In the question, we are given a capsule structure of a capsule with a cylinder in between the two hemispheres. The length of the entire capsule is 14 and the diameter length is 5mm. So, from this we have to find the entire surface area of the capsule.
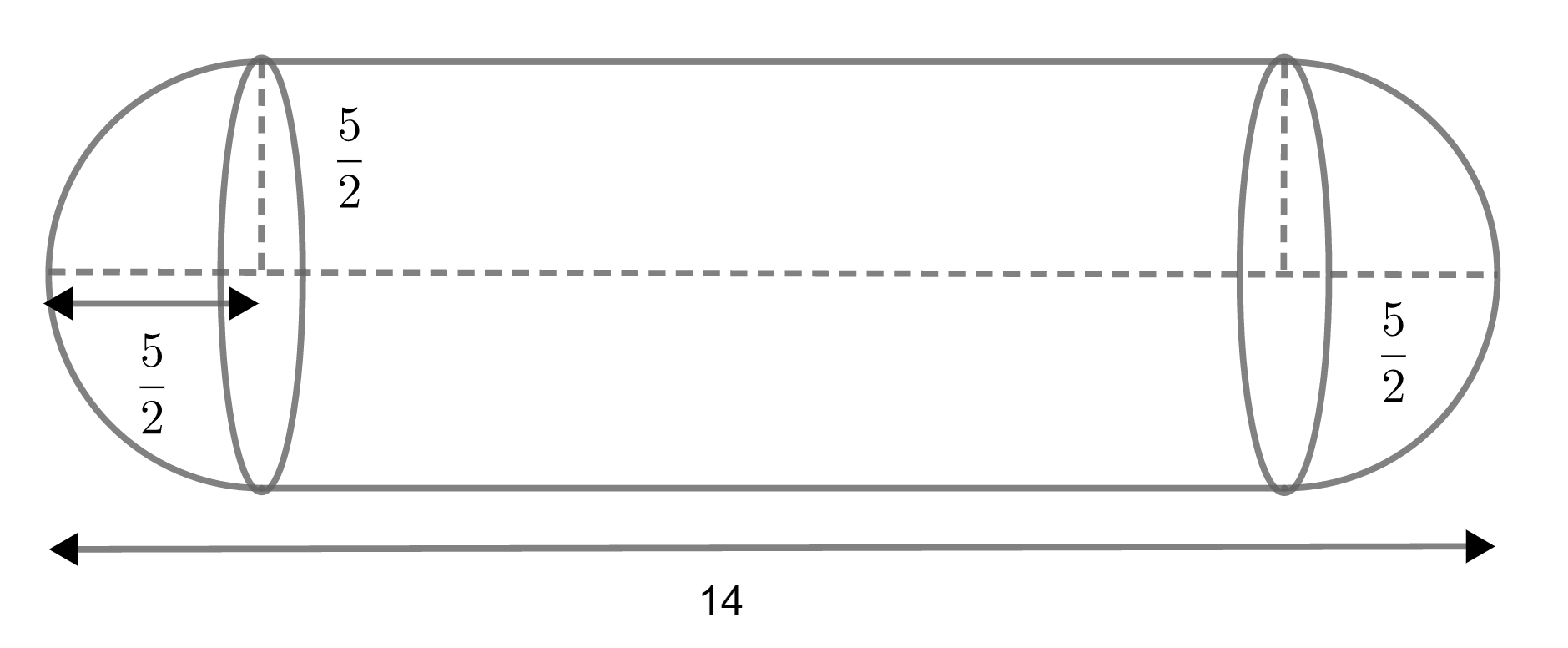
The figure of the capsule is,
Now, to find the curved surface area, we have to find the curved surface area of each of the cylinder and two hemispheres and add them all.
Now, as we are said that, diameter is 5mm then, the radius will be \[\dfrac{5mm}{2}\] as diameter is twice the radius. As the base is shared by both the hemispheres and the cylinder, so, we can say that the radius of the base of the cylinder and that of hemisphere is \[\dfrac{5}{2}mm\].
The total height of the capsule is given as 14mm in which height of hemisphere is also included which is \[\dfrac{5}{2}mm\] . As there were two hemispheres, hence we can say that, total height of two hemisphere are \[\dfrac{5}{2}mm+\dfrac{5}{2}mm\Rightarrow 5mm\].
So, the height of cylinder is \[14mm-5mm\Rightarrow 9mm\]
Now, at first, we will find the curved surface area of the cylinder using formula \[2\pi rh\] where radius is r, h is the height. Hence, on substituting \[r\text{ as }\dfrac{5}{2}mm\text{ and height as 9mm}\] we get,
\[2\pi \times \dfrac{5}{2}mm\times 9mm\Rightarrow \left( 45\pi \right)m{{m}^{2}}\]
For the hemisphere, we will first find a curved surface of 1 and then we will multiply it by 2, to get the total curved surface area of two hemispheres. We can find curved surface area using formula \[2\pi {{r}^{2}}\] So, for two it will be \[2\times 2\pi {{r}^{2}}\Rightarrow 4\pi {{r}^{2}}\] Here, value of \[r\text{ is }\dfrac{5}{2}mm\] Thus, on substituting we get, \[4\times \pi \times \dfrac{5}{2}mm\times \dfrac{5}{2}mm\Rightarrow \left( 25\pi \right)m{{m}^{2}}\]
Now, hence, on adding the area we get,
\[\left( 45\pi +25\pi \right)m{{m}^{2}}\Rightarrow 70\pi m{{m}^{2}}\]
We know that, the value of \[\pi \text{ is }\dfrac{22}{7}\] so, on substituting we get,
\[\left( 70\times \dfrac{22}{7} \right)m{{m}^{2}}\Rightarrow 220m{{m}^{2}}\]
Thus, the surface area is \[220m{{m}^{2}}\]
Note: Students while solving the problem will tend to do the mistake by calculating total surface area of each of the hemispheres using formula \[3\pi {{r}^{2}}\] and cylinder using \[2\pi r\left( r+h \right)\] separately and add. So, be careful about that.
Complete step-by-step answer:
In the question, we are given a capsule structure of a capsule with a cylinder in between the two hemispheres. The length of the entire capsule is 14 and the diameter length is 5mm. So, from this we have to find the entire surface area of the capsule.
The figure of the capsule is,

Now, to find the curved surface area, we have to find the curved surface area of each of the cylinder and two hemispheres and add them all.
Now, as we are said that, diameter is 5mm then, the radius will be \[\dfrac{5mm}{2}\] as diameter is twice the radius. As the base is shared by both the hemispheres and the cylinder, so, we can say that the radius of the base of the cylinder and that of hemisphere is \[\dfrac{5}{2}mm\].
The total height of the capsule is given as 14mm in which height of hemisphere is also included which is \[\dfrac{5}{2}mm\] . As there were two hemispheres, hence we can say that, total height of two hemisphere are \[\dfrac{5}{2}mm+\dfrac{5}{2}mm\Rightarrow 5mm\].
So, the height of cylinder is \[14mm-5mm\Rightarrow 9mm\]
Now, at first, we will find the curved surface area of the cylinder using formula \[2\pi rh\] where radius is r, h is the height. Hence, on substituting \[r\text{ as }\dfrac{5}{2}mm\text{ and height as 9mm}\] we get,
\[2\pi \times \dfrac{5}{2}mm\times 9mm\Rightarrow \left( 45\pi \right)m{{m}^{2}}\]
For the hemisphere, we will first find a curved surface of 1 and then we will multiply it by 2, to get the total curved surface area of two hemispheres. We can find curved surface area using formula \[2\pi {{r}^{2}}\] So, for two it will be \[2\times 2\pi {{r}^{2}}\Rightarrow 4\pi {{r}^{2}}\] Here, value of \[r\text{ is }\dfrac{5}{2}mm\] Thus, on substituting we get, \[4\times \pi \times \dfrac{5}{2}mm\times \dfrac{5}{2}mm\Rightarrow \left( 25\pi \right)m{{m}^{2}}\]
Now, hence, on adding the area we get,
\[\left( 45\pi +25\pi \right)m{{m}^{2}}\Rightarrow 70\pi m{{m}^{2}}\]
We know that, the value of \[\pi \text{ is }\dfrac{22}{7}\] so, on substituting we get,
\[\left( 70\times \dfrac{22}{7} \right)m{{m}^{2}}\Rightarrow 220m{{m}^{2}}\]
Thus, the surface area is \[220m{{m}^{2}}\]
Note: Students while solving the problem will tend to do the mistake by calculating total surface area of each of the hemispheres using formula \[3\pi {{r}^{2}}\] and cylinder using \[2\pi r\left( r+h \right)\] separately and add. So, be careful about that.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
Explain the Treaty of Vienna of 1815 class 10 social science CBSE

The highest dam in India is A Bhakra dam B Tehri dam class 10 social science CBSE

Name the place where the Indian National Congress session class 10 social science CBSE

Name the place where Indian National Congress session class 10 social science CBSE

Name the largest artificial lake that was built in class 10 social science CBSE

Distinguish between coming together federations and class 10 social science CBSE




