Question

A metal pipe has an external radius of 4cm and an internal radius of 3cm. The volume of the metal of length 10cm is:
(a) 120 cubic cm
(b) 220 cubic cm
(c) 440 cubic cm
(d) 225 cubic cm

Answer 1

Hint: A pipe is generally cylindrical in shape and hollow at the centre. To get the answer to the above question find the volume of the inner cylinder and subtract it from the volume of the outer cylinder. Remember that volume of the cuboid is base area multiplied by height, i.e., $ \pi {{r}^{2}}l $ , where r is the radius of the base which is a circle and l is the length.

Complete step-by-step answer:
To start with the question let us draw the diagram of the pipe.

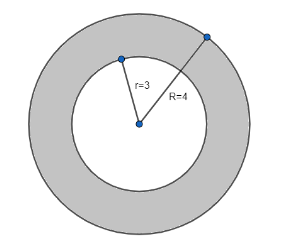
The above diagram shows the view of the pipe if we see it from one end.
Now first let us find the inner volume of the cylindrical pipe. It is given that the inner radius of the base is 3 cm and length of the pipe is 10 cm. We also know that the volume of the cylinder is base area multiplied by height, i.e., $ \pi {{r}^{2}}l $ , where r is the radius of the base which is a circle and l is the length.
\[\text{Inner volume =}\pi {{\text{r}}^{2}}l=\pi \times {{3}^{2}}\times 10=90\pi \text{ }c{{m}^{3}}\] .
Also, the outer volume can be found using the outer radius of the base, which is equal to 4 cm. l in this case also remains the same.
 $ \text{Outer volume}=\pi {{\text{r}}^{2}}l=\pi \times {{4}^{2}}\times 10=160\pi \text{ }c{{m}^{3}} $
We can also see from the figure that the volume of the pipe is inner volume subtracted from the outer volume, as inner volume is hollow. So, using the above results we can say that:
\[\text{Volume of pipe}=160\pi -90\pi =70\pi \text{ c}{{\text{m}}^{3}}\]
Now we will put the value $ \pi =\dfrac{22}{7} $ . On doing so, we get
\[\text{Volume of pipe}=70\pi =70\times \dfrac{22}{7}=220\text{ c}{{\text{m}}^{3}}\]
Therefore, the answer to the above question is option (b).

Note: Remembering the formula for volume, surface area and other specific things relate to standard three dimensional figures like cylinder is very important. The first thing to keep in mind in such questions is draw a diagram and figure out the volumes of the parts that are to be considered and the parts whose volumes are to be subtracted, for this you might have to select the view of the object given which best serves your objective, as we choose the top view in the above question. Also, be careful about the calculation part as there is a high chance of making a mistake in the calculation part.