
A multi-range voltmeter can be constructed by using a galvanometer circuit as shown in the figure. We want to construct a voltmeter that can measure
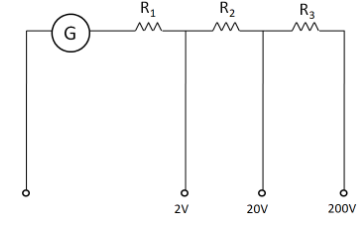

Answer
480.9k+ views
Hint : To solve this question we have to separately consider each of the three voltmeters. Then, applying the Ohm’s law to each circuit thus obtained, we can get the respective values of the resistances.
Complete step by step answer
Since the resistance of the galvanometer is given in the question to be equal to
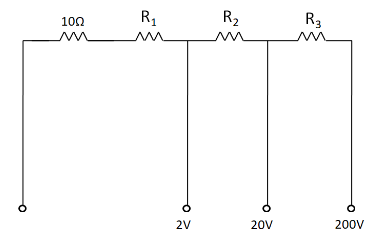
Considering the first voltmeter which can be used to measure a voltage of
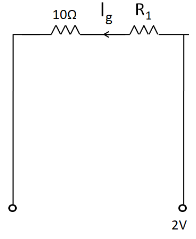
Since the maximum deflection of the galvanometer occurs for a current of
The net resistance in the circuit is given by
Also, the voltage across this resistance is equal to
Multiplying both sides by
Subtracting
Now, we consider the second voltmeter which can measure a voltage of
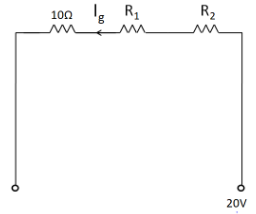
The net resistance in the circuit is
The voltage across the circuit is
So we have
Multiplying both sides by
Substituting (1) we get
Finally, we consider the second voltmeter which can measure a voltage of
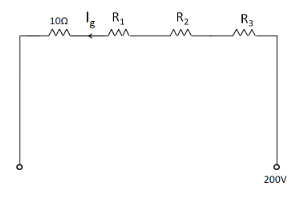
The net resistance in the circuit is
The voltage across the circuit is
So we have
Multiplying both sides by
Substituting (1) and (2) we get
Hence, the value of
Note
We should not forget to convert the value of maximum deflection current into the SI unit. Also, the voltage of the left terminal which is connected to the galvanometer is not given. So we have assumed it to be equal to zero volts. This is because then only the voltmeter will measure the respective voltages given in the question.
Complete step by step answer
Since the resistance of the galvanometer is given in the question to be equal to

Considering the first voltmeter which can be used to measure a voltage of

Since the maximum deflection of the galvanometer occurs for a current of
The net resistance in the circuit is given by
Also, the voltage across this resistance is equal to
Multiplying both sides by
Subtracting
Now, we consider the second voltmeter which can measure a voltage of

The net resistance in the circuit is
The voltage across the circuit is
So we have
Multiplying both sides by
Substituting (1) we get
Finally, we consider the second voltmeter which can measure a voltage of

The net resistance in the circuit is
The voltage across the circuit is
So we have
Multiplying both sides by
Substituting (1) and (2) we get
Hence, the value of
Note
We should not forget to convert the value of maximum deflection current into the SI unit. Also, the voltage of the left terminal which is connected to the galvanometer is not given. So we have assumed it to be equal to zero volts. This is because then only the voltmeter will measure the respective voltages given in the question.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




