Question

A non conducting disc of radius \[R\], charge \[q\] is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity \[\omega \], charge \[q\] is uniformly distributed over its surface. The magnetic moment of the disc is:
A. \[\dfrac{1}{4}q\omega {R^2}\]
B. \[\dfrac{1}{2}q\omega R\]
C. \[q\omega R\]
D. \[\dfrac{1}{2}q\omega {R^2}\]

Answer 1

Hint:To find the magnetic moment of the disc, first recall the formula for magnetic moment of a current loop. Take a small annular region of the disc and find the magnetic moment of this region and then integrate the value taking the limit of radius from zero to \[R\], to find the value of magnetic moment of the whole disc.

Complete step by step answer:
Given, radius of a non conducting disc, \[R\]. Charge on the disc, \[q\]. Angular velocity of the disc, \[\omega \]. The magnetic moment of a current loop is given by the formula,
\[\mu = IA\]
where \[I\] is the current through the loop and \[A\] is the area of the loop.
Surface charge density is defined as charge per unit area. Here, area of the disc is \[\pi {R^2}\] and charge is \[q\] so, surface charge density will be,
\[\sigma = \dfrac{q}{{\pi {R^2}}}\] (i)
Now, we take a small cross section such that its length is \[dr\] with its inner radius is \[r\] and outer radius is \[r + dr\] and \[dr < < r\].

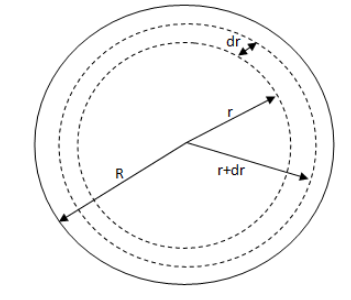
Here, surface charge density for this region will be,
\[\sigma = \dfrac{{dq}}{{d\left( {\pi {r^2}} \right)}}\]
\[ \Rightarrow \sigma = \dfrac{{dq}}{{2\pi rdr}}\]
\[ \Rightarrow dq = 2\pi rdr\sigma \]
Putting the value of \[\sigma \] in the above equation we get,
\[dq = 2\pi rdr\left( {\dfrac{q}{{\pi {R^2}}}} \right)\]
\[ \Rightarrow dq = \dfrac{{2q}}{{{R^2}}}rdr\]
The charge \[dq\] completes one revolution in the time interval, \[T = \dfrac{{2\pi }}{\omega }\]
We know current is charge per unit time. So here current through this small region will be,
\[dI = \dfrac{{dq}}{T}\]
Putting the values of \[dq\] and \[T\] we get,
\[dI = \dfrac{{\left( {\dfrac{{2q}}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{{2\pi }}{\omega }} \right)}}\]
\[ \Rightarrow dI = \dfrac{{\left( {\dfrac{q}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{\pi }{\omega }} \right)}}\] (ii)

Area enclosed by this current is \[A = \pi {r^2}\]
So, magnetic moment due to this loop will be, (using equation (i))
\[d\mu = dI \times A\]
Putting the value of \[dI\] and \[A\] we get,
\[d\mu = \dfrac{{\left( {\dfrac{q}{{{R^2}}}rdr} \right)}}{{\left( {\dfrac{\pi }{\omega }} \right)}} \times \pi {r^2}\]
\[ \Rightarrow d\mu = \dfrac{{\omega q}}{{{R^2}}}rdr \times {r^2}\]
\[ \Rightarrow d\mu = \dfrac{{\omega q}}{{{R^2}}}{r^3}dr\]
Now, we get the magnetic moment of the disc by integrating on both sides of the above equation from \[0\] to \[R\] on right side and \[0\] to \[\mu \] on left side,
\[\int\limits_0^\mu {d\mu } = \int\limits_0^R {\dfrac{{\omega q}}{{{R^2}}}{r^3}dr} \]
\[ \Rightarrow \mu = \dfrac{{\omega q}}{{{R^2}}}\left[ {\dfrac{{{r^4}}}{4}} \right]_0^R\]
\[ \Rightarrow \mu = \dfrac{{\omega q}}{{{R^2}}}\left[ {\dfrac{{{R^4}}}{4}} \right]\]
\[ \therefore \mu = \dfrac{1}{4}q\omega {R^2}\]
Therefore, the magnetic moment of the disc is \[\dfrac{1}{4}q\omega {R^2}\].

Hence, the correct answer is option A.

Note: The magnetic moment can be defined as the magnetic strength and orientation of an object that produces a magnetic field. It is a vector quantity and direction of magnetic moment can be found using right hand rule, which is perpendicular to the current loop.