Question

A normal chord of the parabola \[{{y}^{2}}=4x\] subtending a right angle at the vertex makes an acute angle \[\theta \] with the x –axis, then \[\theta \] is
(a)\[{{\tan }^{-1}}2\]
(b)\[{{\sec }^{-1}}\left( \sqrt{3} \right)\]
(c)\[{{\cot }^{-1}}\left( \sqrt{3} \right)\]
(d)None

Answer 1

Hint: Use the property of two perpendicular lines with respect to slopes of them.
Product of slopes of two perpendicular lines = -1.

Complete step-by-step answer:
Suppose two points of the normal chord lying on parabola as \[\left( t_{1}^{2},2{{t}_{1}} \right)\] and \[\left( t_{2}^{2},2{{t}_{2}} \right)\]. Get the slope of the chord by differentiating the curve (Parabola) at the point where normal is drawn. Get the slope of a line using the relation,
\[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\], where \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the points lying on the line.

As we need to find the angle \[\theta \] formed (inclination) with the axis of parabola, \[{{y}^{2}}=4ax\] with the help of given in formations in the problem.
We know the axis of parabola \[{{y}^{2}}=4ax\] is x – axis, as it is symmetric about x – axis. So, we need to determine the angle with the x – axis. So we can calculate the slope of the chord and equate it to the \[\tan \theta \] because slope is defined as tan of angle formed with the positive direction of x –axis.
So, let us suppose slope of normal chord = \[\tan \theta \]
As, we need to find the slope of a chord of, which is normal at one end and subtends a right angle at the origin as well. So, let the two ends of the chord are \[\left( t_{1}^{2},2{{t}_{1}} \right)\] and \[\left( t_{2}^{2},2{{t}_{2}} \right)\]. [Parametric coordinates for \[{{y}^{2}}=4ax\] is given as \[a{{t}^{2}},2at\]].
So, diagram can be represented as,

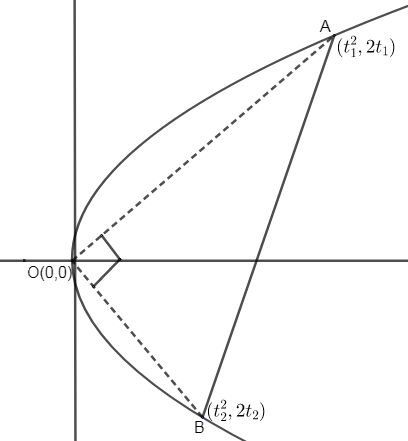
Let AB is acting as a normal at the point B.
We know the slope of tangent at point B can be given as,
\[{{\left. \dfrac{dy}{dx} \right|}_{\left( at_{2}^{2},2a{{t}_{2}} \right)}}-(i)\]
Where, we need to use relation, \[{{y}^{2}}=4x\].
So, differentiating, \[{{y}^{2}}=4x\], we get,
\[\begin{align}
  & \dfrac{d}{dx}{{y}^{2}}=\dfrac{d}{dx}\left( 4.x \right) \\
 & 2y\dfrac{dy}{dx}=4 \\
\end{align}\]
Where, we know,
\[\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}\]
Hence, we get,
\[\begin{align}
  & y\dfrac{dy}{dx}=2 \\
 & \dfrac{dy}{dx}=\dfrac{2}{y} \\
\end{align}\]
Now, we can get slope of tangent at point B as,

\[{{\left. \dfrac{dy}{dx} \right|}_{\left( t_{2}^{2},2{{t}_{2}} \right)}}=\dfrac{2}{2{{t}_{2}}}=\dfrac{1}{{{t}_{2}}}-(ii)\]
Now, we know tangent is perpendicular to the normal at the point of tangency for any conic. And as, we know the relation between slope of two perpendicular lines is given as,
Product of two perpendicular lines = -1 – (iii)
So, we get,
Slope of normal at BX slope of tangent at B = -1.
\[\dfrac{1}{{{t}_{2}}}\times \] slope of normal at B = -1
Slope of normal at B = \[-{{t}_{2}}\]
Now, we can calculate slope of normal at B i.e. slope of line AB by formula,
Slope = \[\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}-(iv)\]
So, we get,
Slope of normal at B = \[\dfrac{2{{t}_{2}}-2{{t}_{1}}}{t_{2}^{2}-t_{1}^{2}}=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( t_{2}^{2}-t_{1}^{2} \right)}=\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{2}}+{{t}_{1}} \right)\left( {{t}_{2}}-{{t}_{1}} \right)}\]
Slope of normal at B = \[\dfrac{2}{\left( {{t}_{2}}+{{t}_{1}} \right)}\]
As, we have already calculated the slope of normal at point B as \[-{{t}_{2}}\].
 So, we get, \[\dfrac{2}{{{t}_{1}}+{{t}_{2}}}=-{{t}_{2}}\]
\[\begin{align}
  & -2={{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \\
 & {{t}_{1}}{{t}_{2}}+t_{2}^{2}=-2-(v) \\
\end{align}\]
Now, as AO and BO are perpendicular to each other. So, we can calculate the slopes of them and use equation (iii).
So, we get slope of AO from the equation (iv) as,
Slope of AO = \[\dfrac{2{{t}_{1}}-0}{t_{1}^{2}-0}=\dfrac{2{{t}_{1}}}{t_{1}^{2}}=\dfrac{2}{{{t}_{1}}}\]
Similarly, slope of BO = \[\dfrac{2}{{{t}_{2}}}\]
Now, using equation (iii), we get,
\[\begin{align}
  & \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\
 & 4=-{{t}_{1}}{{t}_{2}} \\
\end{align}\]
Or
\[{{t}_{1}}{{t}_{2}}=-4-(vi)\]
Now, putting, \[{{t}_{1}}{{t}_{2}}=-4\] to the equation (v), we get,
\[\begin{align}
  & -4+t_{2}^{2}=-2 \\
 & t_{2}^{2}=4-2=2 \\
 & {{t}_{2}}=\pm \sqrt{2} \\
\end{align}\]
We know the slope of the chord is given as \[-{{t}_{2}}\]. So, the possible slope of the chord is \[\pm \sqrt{2}\].
Hence, \[\pm \sqrt{2}\] is a slope of the normal chord as well.
The slope of the chord is \[\tan \theta \]. So, we can equate \[\pm \sqrt{2}\] to \[\tan \theta \].
So, we get,
\[\begin{align}
  & \tan \theta =\pm \sqrt{2} \\
 & \theta ={{\tan }^{-1}}\left( \pm \sqrt{2} \right) \\
\end{align}\]
As, there are two inclinations of the chord with the x – axis (one with positive direction of x – axis and another with negative direction).
So, we will get two angles by the same chord by the equation, \[\theta ={{\tan }^{-1}}\left( \pm \sqrt{2} \right)\].
Hence, the inclination can also be said as \[{{\tan }^{-1}}\left( \sqrt{2} \right)\] only as well. So, the statement given in the problem is proved.
Now, we get, \[\tan \theta =\sqrt{2}\]
We know, \[\tan \theta =\] Perpendicular / Base
Hence, we can draw a right angle triangle as,

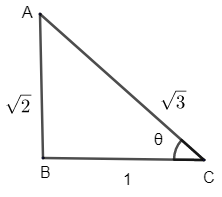
With the help of Pythagoras theorem, we get,
\[\begin{align}
  & {{\left( AC \right)}^{2}}={{\left( \sqrt{2} \right)}^{2}}+{{\left( 1 \right)}^{2}}=3 \\
 & AC=\sqrt{3} \\
\end{align}\]
Hence, we get,
\[\sec \theta \] = Hypotenuse / Base = \[\sqrt{3}\]
Or
\[\theta ={{\sec }^{-1}}\left( \sqrt{3} \right)\]
So, option (b) is the correct answer.

Note: One may use the direct result \[{{t}_{1}}{{t}_{2}}=-4\] for parabola \[{{y}^{2}}=4ax\], if any chord is subtending an angle of \[{{90}^{\circ }}\] at the vertex of the parabola. It can be used for future reference for the given condition in the problem.
One may confuse the option given as they are in different forms. So, check all the options individually. \[{{\tan }^{-1}}\sqrt{2}\] and \[{{\sec }^{-1}}\sqrt{3}\] both are correct but \[{{\tan }^{-1}}\sqrt{2}\] is not given in the question, so, one may tick none of these as correct answer as well, which is wrong. So, be careful with these kinds of options for the problem.