Question

A npn transistor is connected in common emitter configuration in a given amplifier. A load resistance of $800\ \Omega $ is connected in the collector circuit and the voltage drop across it is \[0.8\ \text{V}\]. If the current amplification factor is 0.96 and the input resistance of the circuit is $192\ \Omega $, the voltage gain and the power gain of the amplifier will respectively be
A. 4, 3.84
B. 3.69,3.84
C. 4,4
D. 4,3.69

Answer 1

Hint: The current amplification factor is the ratio of collector current to base current for a transistor in common emitter configuration. For an ideal transistor, the base emitter voltage is 0 for a transistor to be in active mode. Use Kirchhoff's Voltage Law to determine the base current.

Formula Used:
$\beta =\dfrac{{{I}_{c}}}{{{I}_{b}}}$
${{A}_{V}}=\dfrac{{{V}_{out}}}{{{V}_{in}}}$
${{A}_{I}}=\dfrac{{{I}_{out}}}{{{I}_{in}}}$


Complete step by step answer:
The question mentions that the transistor is working in a common emitter configuration. The circuit diagram of the transistor can be seen as below.

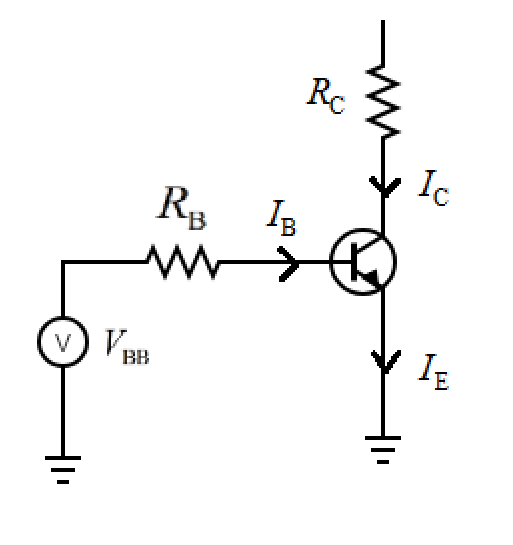
The input terminal for the transistor would be base and the output would be collector. Now, the current amplification factor $\left( \beta \right)$ is the ratio of the output current to the input current. Thus, it can be written as,
\[\begin{align}
  & \beta =\dfrac{{{I}_{c}}}{{{I}_{b}}} \\
 & \dfrac{{{I}_{C}}}{{{I}_{B}}}=0.96
\end{align}\]
Here, ${{I}_{B}}$ is the base current and ${{I}_{C}}$ is the collector current.
Now, since there is nothing mentioned about the transistor, we assume that the transistor is ideal and is working in the forward active region. Now, ideally a saturated transistor acts as a closed switch between the collector and emitter. Thus, there is no need for the base emitter voltage to enable the transistor to work in the active region. Thus, it is assumed that the base emitter voltage or ${{V}_{BE}}=0$ for an ideal transistor. Thus,
${{V}_{B}}={{V}_{E}}=0$
Now, using Ohm's law, the current across the collector would be calculated using the potential drop across the load voltage connected across the collector. Thus,
${{I}_{C}}=\dfrac{{{V}_{L}}}{{{R}_{C}}}$
Here, ${{R}_{C}}$ is the resistance connector to the collector and the ${{V}_{L}}$ is the potential drop across the load resistor ${{R}_{C}}$. The collector current is calculated as,
$\begin{align}
  & {{I}_{C}}=\dfrac{{{V}_{L}}}{{{R}_{C}}} \\
 & =\dfrac{0.8\ \text{V}}{800\ \Omega } \\
 & =1000\ \text{A}
\end{align}$
Now, calculate the value of base current using the current amplification factor.
$\begin{align}
  & {{I}_{B}}=\dfrac{{{I}_{C}}}{\beta } \\
 & =\dfrac{{{10}^{-3}}}{0.96}\ \text{A}
\end{align}$
Kirchhoff’s Voltage law states that for any closed loop the sum of all the potential drops is equal to zero. Now, apply the Kirchhoff’s voltage law to calculate the input voltage i.e. ${{V}_{B}}$.
$\begin{align}
  & -{{V}_{B}}+{{I}_{B}}{{R}_{B}}=0 \\
 & {{V}_{B}}={{I}_{B}}{{R}_{B}} \\
 & =\dfrac{{{10}^{-3}}}{0.96}\times 192 \\
 & =0.2\ \text{V}
\end{align}$
Now, the voltage gain is the ratio of output voltage to the input voltage. It is calculated as,
$\begin{align}
  & {{A}_{V}}=\dfrac{{{V}_{out}}}{{{V}_{in}}} \\
 & =\dfrac{{{V}_{L}}}{{{V}_{B}}} \\
 & =\dfrac{0.8}{0.2} \\
 & =4
\end{align}$
Now, calculate the current gain using the output current and input current.
$\begin{align}
  & {{A}_{I}}=\dfrac{{{I}_{out}}}{{{I}_{in}}} \\
 & =\dfrac{{{I}_{C}}}{{{I}_{B}}} \\
 & =0.96
\end{align}$
The power gain is calculated as the product of voltage gain and current gain.
$\begin{align}
  & {{A}_{P}}={{A}_{V}}{{A}_{I}} \\
 & =4\times 0.96 \\
 & =3.84
\end{align}$
The voltage gain and power gain are 4 and 3.84 respectively. Thus, the correct option is (A).

Note: The current across the load resistor can be calculated using the potential drop across the load voltage. Use the Kirchhoff law correctly to calculate the base voltage. The base emitter voltage is assumed as zero for an ideal transistor.