Question

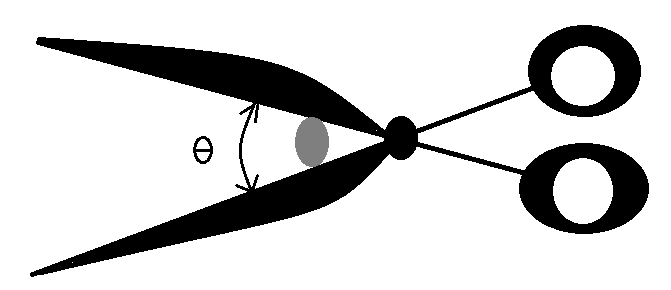
A pair of scissors is used to cut a wire of circular cross-section held vertically. To reduce required force the wire must be placed close to the hinge; but if it is placed close to the hinge, it slides away from the hinge until the angle between the blades becomes θ. Find the coefficient of friction between the blades and the wire

A. \[\cot \left( {0.5\theta } \right)\]
B. $\tan \left( {0.5\theta } \right)$
C. $0.5\tan \theta $
D. Insufficient data

Answer 1

Hint: The Normal act perpendicular to the point of contact. The frictional force between two objects always acts at the point of contact. If a body is in equilibrium then all the forces need to balance out each other because the resulting force in any direction would set a body in motion.

Complete step by step answer:
In this question, it is given that while we apply force for cutting the wire, the wire rolls away and thus there is an angle $\theta $ is formed between the tongs of the scissors
Here the particle will try to move away from the scissor and the frictional force will act in the opposite direction.
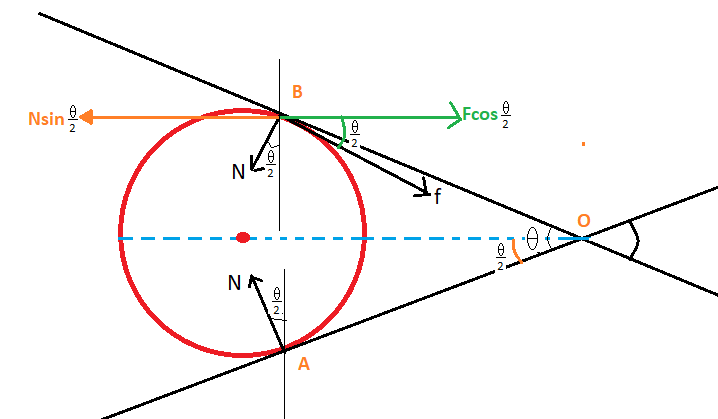
We will draw the free body diagram

Here,
Let after the motion the wire rest at a position shown in the figure
There will be two points of contact A and B
At A the angle of contact be $\left( {\dfrac{\theta }{2}} \right)$ and the angle will same at point B also due to symmetry
Now the force $f$ will act along with the point of contact of wire.
Now we will resolve the forces into a perpendicular axis
$f\cos \dfrac{\theta }{2}$ for force $f$
And $N\sin \dfrac{\theta }{2}$ for normal $N$

Now one component of each friction force and normal force will be the axis shown in the figure and will be opposite in direction as they are acting away from each other
As we know the frictional force is given by
$f = \mu N$
Where
$\mu $ the coefficient of friction
$N$ the normal force

We can see in the figure that angle at B will be equal to the angle at O i.e$\dfrac{\theta }{2}$ due to vertically opposite angle property
Now it is clear that for the wire to be in equilibrium the two forces should be equal in magnitude so there would be no resultant force will be there to cause motion
Equating forces, we get
$
  N\sin \dfrac{\theta }{2} = f\cos \dfrac{\theta }{2} \\
  \because f = \mu N \\
  \therefore N\sin \dfrac{\theta }{2} = \mu N\cos \dfrac{\theta }{2} \\
   \Rightarrow \mu = \tan \dfrac{\theta }{2} \\
   \Rightarrow \mu = \tan \left( {0.5\theta } \right) \\
 $

Hence, the correct answer is option (B).

Note: The value of the normal force will always be equal to the product of the coefficient of friction and applied force. For a body to be in equilibrium the net effect of all the forces along all the directions should be zero. The force of friction always acts along with the point of contact.