Question

A panda with a mass M lies without moving on a ramp that is inclined at $\theta $ degrees. The coefficient of static friction between the ramp and the panda is$\mu $. What is the magnitude of the frictional force on the panda?

A. 0
B. $Mg\sin \theta $
C. $\mu Mg\sin \theta $
D. $\mu Mg\cos \theta $
E. $Mg\cos \theta $

Answer 1

Hint: As a first step, you could read the question well and thus understand the situation properly. Then you could make a neat free body diagram marking all the forces acting on the panda which would be due to the weight of the panda and the frictional force on it. Now, by balancing accordingly we will get the magnitude of the frictional force.

Complete answer:
In the question, we are given a plane that is inclined at an angle$\theta $. $\mu $ is the coefficient of static friction between the ramp and the panda. We are supposed to find the magnitude of frictional force on the panda.
In order to solve this problem, let us first make the free body diagram of the given situation with all the forces acting on the panda marked.

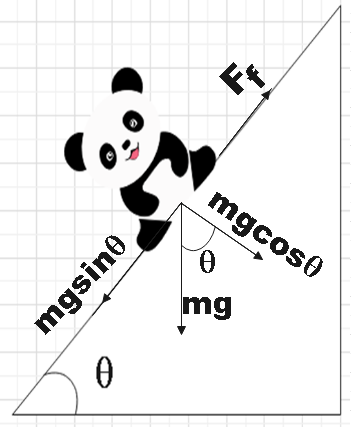
We see that the weight of the panda is acting downwards and we could resolve this into its components and we see that the sine component of this force balances the frictional force acting on the panda. That is,
$mg\sin \theta ={{F}_{f}}$
Hence, we found the magnitude of the frictional force on the panda to be,
 ${{F}_{f}}=mg\sin \theta $

Note:
From the figure, we could also conclude that the cosine component of the weight of the panda is balanced by the Normal force acting on it. Also, we would expect the coefficient of friction to be present in the expression for frictional force but here the force is being balanced by the sine component so as to keep the panda at rest.