Question

A parallel beam of monochromatic light of wavelength $\lambda $ is used in Young’s double-slit experiment. The slits are separated by a distance $d$ and the screen is placed parallel to the plane of the slits. The incident beam makes an angle $\theta = {\sin ^{ - 1}}\left( {\dfrac{\lambda }{{2d}}} \right)$ with the normal to the plane of the slits. A transparent sheet of refractive index $\prime \mu \prime $ and thickness $t = \dfrac{\lambda }{{2\left( {\mu - 1} \right)}}$ is introduced in front of one of the slit. Find the intensity at the geometrical centre.

Answer 1

Hint: In Young's double-slit experiment, we have two slits separated by a distance. Two coherent sources will produce an interference pattern. This will create alternate bright and dark fringes. The separation between the two consecutive bright fringes is called the fringe width.

Complete Step by step solution:
The setup of the experiment is shown in the diagram below

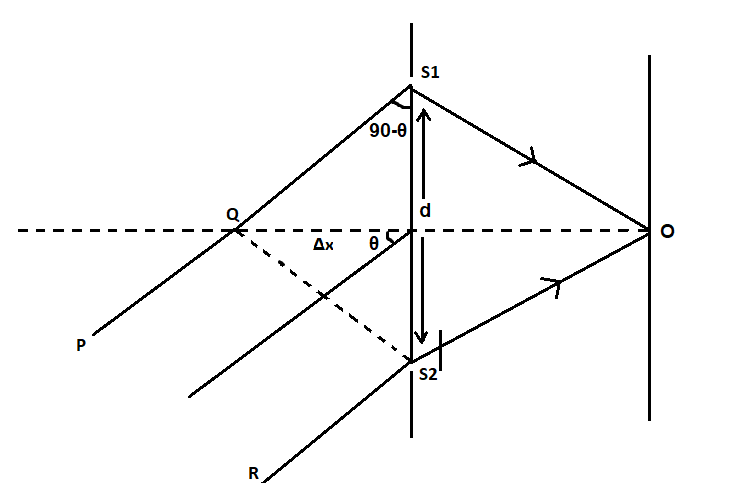
As shown in the figure, $O$ is the centre of the screen, ${S_1}$ snd ${S_2}$ are the slits.
The distance between the two slits is $d$ and the screen is placed at a distance $D$ from the slits.
The incident light beam makes an angle $\theta $ with the normal to the plane of the slits.
Due to the introduction of the transparent sheet of the refractive index $\prime \mu \prime $ and thickness $t = \dfrac{\lambda }{{2\left( {\mu - 1} \right)}}$ , there will be a path difference.
The path difference of the two incident beams before reaching the slits is shown as $\Delta x$.
The path travelled by the first beam can be written as, $PQ + Q{S_1} + {S_1}O$
The path travelled by the second beam can be written as, $R{S_2} + {S_2}O - t + \mu t$
where $\mu $ is the refractive index of the transparent sheet and $t$ is the thickness of the sheet.
Then, the total path difference can be written as,
Path difference $ = PQ + Q{S_1} + {S_1}O - \left( {R{S_2} + {S_2}O - t + \mu t} \right)$
This can be rearranged as
Path difference $ = PQ - R{S_2} + Q{S_1} + {S_1}O - {S_2}O + t - \mu t$
We know that $PQ = R{S_2}$, $\therefore PQ - R{S_2} = 0$ and $Q{S_1} = \Delta x$
${S_1}O - {S_2}O = 0$ because $O$ is the geometric centre.
Substituting all this, we get
Path difference $ = 0 + \Delta x + 0 + t - \mu t$
Thus we can write that
Path difference, $ = \Delta x - \left( {\mu - 1} \right)t$
If the transparent sheet is placed on the other side then the path difference will be,
Path difference $ = PQ + Q{S_1} + {S_1}O - t + \mu t - \left( {R{S_2} + {S_2}O} \right)$
Again substituting the values we get
Path difference $ = 0 + \Delta x + 0 + t\left( {\mu - 1} \right)$
This can be written as,
Path difference $ = \Delta x + t\left( {\mu - 1} \right)$
Therefore the total path difference $ = \Delta x \pm {P_{ts}}$
where ${P_{ts}}$ is the path difference due to the transparent sheet.
i.e. path difference $ = \Delta x \pm t\left( {\mu - 1} \right)$
From the figure, if we take $\sin \theta = \dfrac{{\Delta x}}{d}$
From this, we can take, $d\sin \theta = \Delta x$.
In the question, it is given that $\theta = {\sin ^{ - 1}}\left( {\dfrac{\lambda }{{2d}}} \right)$
Substituting this value of $\theta $ in the above equation, we get
$\Delta x = d\sin {\sin ^{ - 1}}\left( {\dfrac{\lambda }{{2d}}} \right) = \dfrac{{d\lambda }}{{2d}} = \dfrac{\lambda }{2}$
The thickness of the transparent sheet is given as, $t = \dfrac{\lambda }{{2\left( {\mu - 1} \right)}}$
From this $t\left( {\mu - 1} \right) = \dfrac{\lambda }{{2\left( {\mu - 1} \right)}}\left( {\mu - 1} \right) = \dfrac{\lambda }{2}$
Now the phase difference can be written as,
$\Phi = \dfrac{{2\pi }}{\lambda }\Delta x \pm \dfrac{{2\pi }}{\lambda }{P_{ts}}$
That can be written as,
$\Phi = \dfrac{{2\pi }}{\lambda }\dfrac{\lambda }{2} \pm \dfrac{{2\pi }}{\lambda }\dfrac{\lambda }{2}$
This will become,
$\Phi = \pi \pm \pi \Rightarrow 2\pi ,0$
We know that when the phase difference is $\Phi = 2n\pi $ where $n = 0,1,2.....$ constructive interference is taking place. This means that the intensity will be maximum. Therefore the intensity at the geometric centre will be maximum.

Note:
When two light beams of the same phase interfere with each other a maximum intensity is obtained and this type of interference is called constructive interference. When two beams of opposite phases interfere and the intensity is reduced, this type of interference is called destructive interference.