Question

What is a parallel plate capacitor? Deduce the expression for the capacitance when a dielectric slab is inserted between its plates. Assume that slab thickness is less than the plate separation. Also find the expression for energy stored per unit volume of a capacitor.

Answer 1

Hint: Capacitance of a capacitor is defined as its ability to store electrical energy in form of charge. Mathematically, It's the ratio of charge on one plate to potential difference between conductors.
To deduce expression for the capacitance, calculate voltage between both the plates by determining electric field and substitute in capacitance formula.
Formula Used:
Capacitance, $C=\dfrac{Q}{V}$

Complete answer:
A parallel plate capacitor is a system of two conducting plates each of area A, having charges +Q and –Q and separated by a small distance, d. This setup is used to store charge.
Capacitance of a capacitor is its ability to store charge and is given by
$C=\dfrac{Q}{V}$
Where Q is charged on each conductor and V is the potential between them.
Let us obtain expression for a parallel plate capacitor with a dielectric inserted between its plates.
Consider a parallel plate capacitor with plate area, A and separation between plates, d. Let us assume that a thin dielectric of thickness t is inserted between the plates.

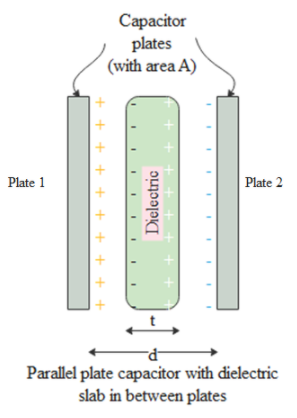
If Q and –Q are the charges on plate 1 and plate 2 respectively, the electric field between the plates outside the dielectric is
${{E}_{0}}=$Electric field due to plate 1 + Electric field due to plate 2
${{E}_{0}}=\dfrac{Q}{2{{\epsilon }_{0}}A}+\dfrac{Q}{2{{\epsilon }_{0}}A}=\dfrac{Q}{{{\epsilon }_{0}}A}$
Where $\epsilon_0$ is the permittivity of free space
Electric field between the plates inside the dielectric is
${{E}_{d}}=\dfrac{{{E}_{0}}}{K}$ where K is the dielectric constant
So the net potential between the plates is,
$V={{E}_{0}}(d-t)+{{E}_{d}}(t)$
$V={{E}_{0}}(d-t)+\dfrac{{{E}_{0}}}{K}t$
Since ${{E}_{0}}=\dfrac{Q}{{{\epsilon }_{0}}A}$
$V=\dfrac{Q}{{{\epsilon }_{0}}A}\left( d-t+\dfrac{t}{K} \right)$
The capacitance of parallel plate capacitor is,
$C=\dfrac{Q}{V}$
$C=\dfrac{{{\epsilon }_{0}}A}{\left( d-t+\dfrac{t}{K} \right)}$
Now let’s obtain an expression for energy stored per unit volume of the capacitor. The parallel plate capacitor is placed in vacuum, then

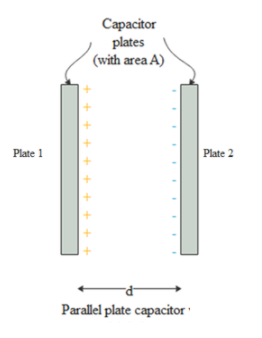
The force on plate 2 due to plate 1 is given by
${{F}_{21}}=\dfrac{{{Q}^{2}}}{2{{\epsilon }_{0}}A}$
Work done to displace the plate from its fixed position is,
$W={{F}_{21}}d$
$W=\dfrac{{{Q}^{2}}}{2{{\epsilon }_{0}}A}d=\dfrac{{{Q}^{2}}}{2C}$
Work done is equal to increase in energy of the system,
$\therefore U=\dfrac{{{Q}^{2}}}{2C}$
Volume in which electric field is created is given by $V=Ad$
So energy stored per unit volume is given by,
$u=\dfrac{U}{V}=\dfrac{{{Q}^{2}}d/2{{\epsilon }_{0}}A}{Ad}$
$u=\dfrac{{{Q}^{2}}}{2{{\epsilon }_{0}}{{A}^{2}}}=\dfrac{1}{2}{{\epsilon }_{0}}{{\left( \dfrac{Q}{{{\epsilon }_{0}}A} \right)}^{2}}$
Since electric field intensity is $E=\dfrac{Q}{{{\epsilon }_{0}}A}$
$u=\dfrac{1}{2}{{\epsilon }_{0}}{{E}^{2}}$

Note:
When a dielectric of thickness equal to separation between the plates of the parallel plate capacitor is inserted, the capacitance of the capacitor increases by a multiple of the dielectric constant. If C and C’ are the capacitance without dielectric and with dielectric respectively then,
$C'=KC$