
A parallelepiped is formed by planes drawn through the points
Answer
503.1k+ views
1 likes
Hint: For solving this question first we will draw planes through the points
Complete step by step solution:
Given:
We have to find the length of edges and diagonals of the parallelepiped formed by planes drawn through the points
Now, before we proceed we should know that if there is a point
Now, from the above discussion, we conclude that,

Now, from the above discussion, we conclude that,
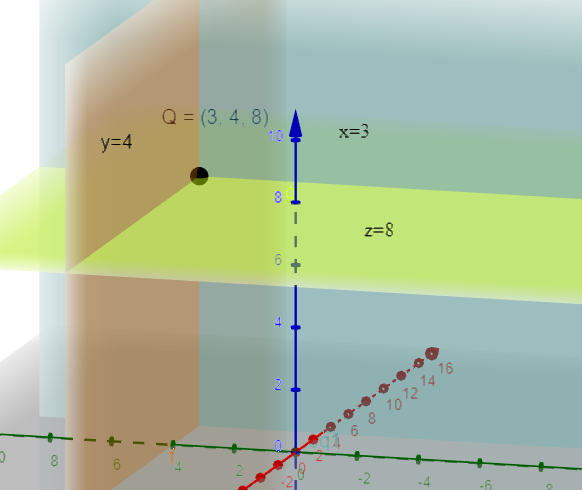
Now, there are the following six planes:
Now, parallelepiped formed by the above six planes will be a cuboid. For more clarity look at the figure given below:
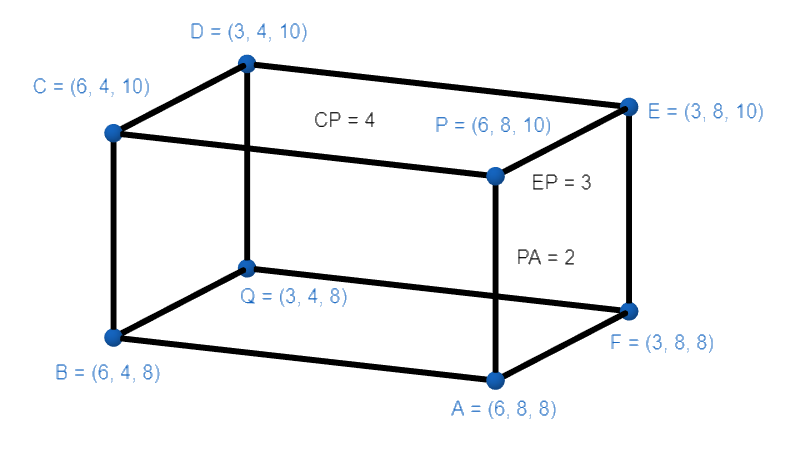
Now, to find the dimensions of the cuboid we will find the distance between the following planes:
Now, as the above three pairs of planes are parallel so, we will simply find the difference in their values.
For length find the distance between planes
Now, from the above result, we conclude that the length, breadth and height of the cuboid will be 4, 3 and 2 units respectively.
Now, as we know that length of the body diagonal of the cuboid of length
Length of the body diagonal
Now, we conclude that the required parallelepiped will be a cuboid of length, breadth and height of the cuboid will be 4, 3 and 2 units respectively and length of the diagonal of the parallelepiped will be
Note: The coordinates of the vertices of the parallelepiped can be found out by finding the point of intersection of the planes taken 3 at a time. For example, the point of intersection of the planes x=6, y=8 and z=10 is (6,8,10), which is the coordinate of the vertex P.
Complete step by step solution:
Given:
We have to find the length of edges and diagonals of the parallelepiped formed by planes drawn through the points
Now, before we proceed we should know that if there is a point
Now, from the above discussion, we conclude that,

Now, from the above discussion, we conclude that,

Now, there are the following six planes:
Now, parallelepiped formed by the above six planes will be a cuboid. For more clarity look at the figure given below:

Now, to find the dimensions of the cuboid we will find the distance between the following planes:
Now, as the above three pairs of planes are parallel so, we will simply find the difference in their values.
For length find the distance between planes
Now, from the above result, we conclude that the length, breadth and height of the cuboid will be 4, 3 and 2 units respectively.
Now, as we know that length of the body diagonal of the cuboid of length
Length of the body diagonal
Now, we conclude that the required parallelepiped will be a cuboid of length, breadth and height of the cuboid will be 4, 3 and 2 units respectively and length of the diagonal of the parallelepiped will be
Note: The coordinates of the vertices of the parallelepiped can be found out by finding the point of intersection of the planes taken 3 at a time. For example, the point of intersection of the planes x=6, y=8 and z=10 is (6,8,10), which is the coordinate of the vertex P.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




