Question

A particle A suffers an oblique elastic collision with a particle B that is at rest initially. If their masses are the same, then after the collision
This question has multiple correct options.
A. Their KE may be equal.
B. A continuous to move in the original direction while B remains at rest.
C. They will move in mutually perpendicular directions.
D. A comes to rest and B starts moving in the direction of the original motion of A2.

Answer 1

Hint: In an oblique collision the particle at rest will gain a velocity perpendicular to that of the incident particle. And because the collision is elastic the total momentum, as well as the kinetic energy of the system, will remain conserved. Using these facts choose the correct options.

Complete step-by-step answer:
When the moving particle interacts with another particle that might be at rest or in motion in terms of physical contact, this phenomenon is known as a collision. A collision in which there is no loss of kinetic energy by the entire system is known as an elastic collision.
If the moving particle collides with another particle such that the particle at rest gains a velocity that is perpendicular to that of the incident particle then that collision is referred to as an oblique collision. The following diagram shows an elastic oblique collision.

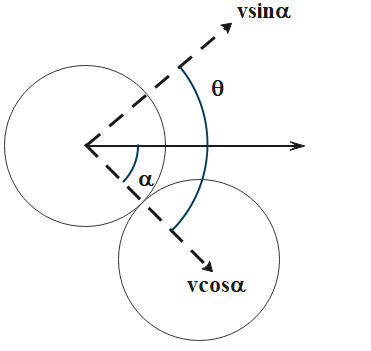
By law of conservation of momentum we know that the momentum of the system before and after collision must remain the same i.e., the total momentum of the system must remain conserved. So we have:
$\eqalign{
  & \vec P = {{\vec P}_1} + {{\vec P}_2} \cr
  & {\left| P \right|^2} = {\left| {{P_1}} \right|^2} + {\left| {{P_2}} \right|^2} + 2{P_1}{P_2}\cos \theta \cdots \cdots \cdots \left( 1 \right) \cr} $

By law of conservation of energy we know that the initial kinetic energy before collision must be equal to the final kinetic energy after collision. So we have:
$\eqalign{
  & \dfrac{{{P^2}}}{{2m}} = \dfrac{{P_1^2}}{{2m}} + \dfrac{{P_2^2}}{{2m}}{\text{ }}\left[ {\because K.E = \dfrac{1}{2}m{v^2}{\text{ and }}P = mv} \right] \cr
  & \Rightarrow {P^2} = P_1^2 + P_2^2 \cdots \cdots \left( 2 \right) \cr} $
Both equation (1) and (2) are only possible if
 $\eqalign{
  & \cos \theta = {0^ \circ } \cr
  & \Rightarrow \theta = {90^ \circ } \cr} $
Hence both the particles must move at right angles to each other after collision.
Now, option A is true because the mass is the same and after impact, the velocity along the line of impact gets exchanged and velocity perpendicular to the line of the impact remains the same or unchanged.
$ \Rightarrow \alpha = {45^ \circ }$
Thus the speeds of the two-particle will remain the same, which in turn means the kinetic energy will remain the same.
Options B and D are clearly false as shown in the figure because both particles A and B keep moving in a mutually perpendicular direction. So option C is true.

Therefore, the correct options are A and C.

Note: Students should make sure to not confuse the difference between elastic and oblique collision. Both these terms have their own significance. There are other types of collisions as well like perfectly elastic, inelastic, and perfectly inelastic collisions. In a perfectly elastic collision, the kinetic energy, as well as the momentum of the system, is conserved. While in an inelastic only the momentum is conserved, and not the kinetic energy.