
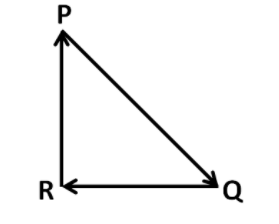
A particle moving with a velocity bar $V$ is acted by three forces shown by the vector triangle PQR. The velocity of the particle will:
(A) Increase
(B) Decrease
(C) Remain constant
(D) Change according to the smallest force.
Answer
140.1k+ views
Hint: To solve this question, we need to use the triangular law of vector addition to calculate the net resultant force of the three forces shown in the given vector triangle. Then, using Newton's second law of motion, we can get the final answer.
Formula used: The formula used to solve this question is given by
$F = ma$, here $F$ is the net force acting on a particle of mass $m$ moving with an acceleration of $a$.
Complete step-by-step solution:
For finding the direction of the change of the particle, we need to determine its acceleration. And for determining the acceleration, we must find out the net force acting on the particle. The vector representation of the forces acting on the particle is shown in the given figure. So we can easily find out the resultant force on the particle, using any one of the laws of vector addition. Since the given force vectors are arranged such that the tail of one coincides with the head of the other, so the triangular law will be the most suitable law here.
We take the vectors along the sides PR and QR out of the given vector triangle to obtain their resultant first, as shown in the below diagram.
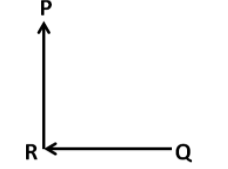
We know that according to the triangular law, the resultant of the two vectors is obtained by joining the head of the first vector with the tail of the other vector. So the resultant of the two vectors along PR and QR can be shown in the below diagram as
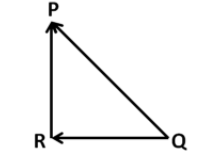
In the given vector triangle, we can see that the force along PQ is just opposite to the resultant of the two vectors along QP. So these two vectors cancel each other giving the net resultant force of the three forces equal to zero.
Thus, the net force acting on the particles is equal to zero. From the Newton’s second law of motion we have
$F = ma$
$ \Rightarrow a = \dfrac{F}{m}$
Since the net force on the particle is zero, so we substitute $F = 0$ in the above equation to get the acceleration of the particle as
$a = 0$
Now, we know that the acceleration is equal to the rate of change of velocity. Since the acceleration is zero, the velocity of the particle will not change.
Hence, the correct answer is option C.
Note: The net resultant force of the three force vectors could also easily be obtained by using the polygon law. Since the three forces in the given vector triangle complete a polynomial in the same order, so their resultant must be zero.
Formula used: The formula used to solve this question is given by
$F = ma$, here $F$ is the net force acting on a particle of mass $m$ moving with an acceleration of $a$.
Complete step-by-step solution:
For finding the direction of the change of the particle, we need to determine its acceleration. And for determining the acceleration, we must find out the net force acting on the particle. The vector representation of the forces acting on the particle is shown in the given figure. So we can easily find out the resultant force on the particle, using any one of the laws of vector addition. Since the given force vectors are arranged such that the tail of one coincides with the head of the other, so the triangular law will be the most suitable law here.
We take the vectors along the sides PR and QR out of the given vector triangle to obtain their resultant first, as shown in the below diagram.

We know that according to the triangular law, the resultant of the two vectors is obtained by joining the head of the first vector with the tail of the other vector. So the resultant of the two vectors along PR and QR can be shown in the below diagram as

In the given vector triangle, we can see that the force along PQ is just opposite to the resultant of the two vectors along QP. So these two vectors cancel each other giving the net resultant force of the three forces equal to zero.
Thus, the net force acting on the particles is equal to zero. From the Newton’s second law of motion we have
$F = ma$
$ \Rightarrow a = \dfrac{F}{m}$
Since the net force on the particle is zero, so we substitute $F = 0$ in the above equation to get the acceleration of the particle as
$a = 0$
Now, we know that the acceleration is equal to the rate of change of velocity. Since the acceleration is zero, the velocity of the particle will not change.
Hence, the correct answer is option C.
Note: The net resultant force of the three force vectors could also easily be obtained by using the polygon law. Since the three forces in the given vector triangle complete a polynomial in the same order, so their resultant must be zero.
Recently Updated Pages
Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




