Question

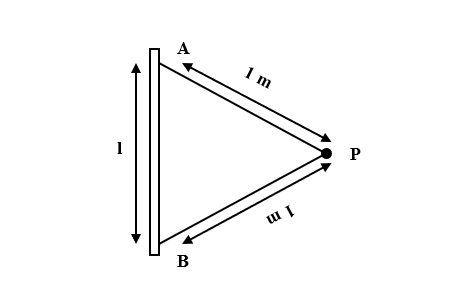
A particle P of mass m attached to a vertical axis by two strings AP and BP of length 1 m each. The separation AB= l. P rotates around the axis with an angular velocity $\omega$. The tension in the two strings are ${T}_{1}$ and ${T}_{2}$. Then,
(This question has multiple correct answers)

A. ${T}_{1}={T}_{2}$
B. ${T}_{1}+{T}_{2}=m {\omega}^{2} l $
C. ${T}_{1}-{T}_{2}= 2mg $
D. BP will remain taut only if $ \omega \geq \sqrt {\dfrac {2g}{l}}$

Answer 1

Hint: To solve this question first find the balancing forces in vertical direction. Then, find the balancing forces in horizontal direction. These balancing forces will be in terms of tension in the string. Then, subtracting these two equations. But the tension in the string along BP has to be greater than zero. So, substitute this condition and find the value for angular velocity.

Complete answer:

Let tension along AB and BP be ${T}_{1}$ and ${T}_{2}$ respectively.
All the sides of the triangle ABP are of the same length. Hence, it is an equilateral triangle and thus, all the angles are the same.
$\angle PAB= \angle ABP= \angle BPA= 60°$
Balancing the forces in vertical direction we get,
${T}_{1}\sin{30°}= {T}_{2}\sin{30°} + mg$
$\Rightarrow {T}_{1}\sin{30°}- {T}_{2}\sin{30°}= mg$
$\Rightarrow \sin{30°} ({T}_{1}-{T}_{2})= mg$
$\Rightarrow \dfrac {1}{2} ({T}_{1}-{T}_{2})= mg$
$\Rightarrow{T}_{1}-{T}_{2}= 2mg$ …(1)
Now, P rotates around the axis with an angular velocity $\omega$. Thus, the forces in horizontal direction is given by,
${T}_{1}\cos{30°}+{T}_{2}\cos{30°}= m{\omega}^{2}r$ …(2)
But, the radius of rotation is given by,
$r= l\cos{30°}$
Substituting above value in equation. (2) we get,
${T}_{1}\cos{30°}+ {T}_{2}\cos{30°}= m{\omega}^{2} l\cos{30°}$
$\Rightarrow \cos{30°} ({T}_{1}+{T}_{2})= m{\omega}^{2} l\cos{30°}$
$\Rightarrow {T}_{1}+{T}_{2}=m {\omega}^{2} l$ …(3)
Subtracting equation. (2) from equation. (3) we get,
${T}_{1}+{T}_{2}- {T}_{1}-{T}_{2}= m {\omega}^{2} l-2mg$
$\Rightarrow 2{T}_{2}= m {\omega}^{2} l-2mg$
To BP to remain taut, ${T}_{2}$ should be greater than zero.
$ m {\omega}^{2} l-2mg > 0$
$\Rightarrow m {\omega}^{2} l \geq 2mg$
$\Rightarrow {\omega}^{2} \geq \dfrac {2mg}{ml}$
$\Rightarrow {\omega}^{2} \geq \dfrac {2g}{l}$
$\Rightarrow \omega \geq \sqrt {\dfrac {2g}{l}}$

Hence, the correct answers are option B, C and D.

Note:
To solve these types of problems, students must analyze the figure and draw the free body diagram first. To draw an appropriate free body diagram, they should know the definition of it. Free body diagrams are diagrams used to show the relative magnitude and direction of all forces acting on the particle or an object in a given situation. It is also known as force diagram as it shows proper position and direction of forces.