Question

A pentagonal prism has 15 edges. How many vertices does it have?
$A.$ 12
$B.$ 10
$C.$ 15
$D.$ 20

Answer 1

Hint – In order to solve this question, we have to use the Euler’s formula that is $V+F-E=2$. By using this formula and with the help of a diagram of pentagonal prism we will get our required answer.

Complete step-by-step answer:

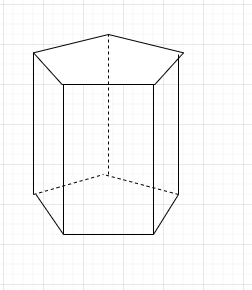
In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges. In this particular question we have to find out the vertices of pentagonal prisms.
In this particular question, we will apply the Euler’s formula that is,
Euler’s formula : $V + F - E = 2$
Where V is the number of vertices
F is number of faces, and
E is the number of edges.
We know that,
Pentagonal prism has 15 edges, and 7 faces
$
   \Rightarrow V = 2 + E - F \\
   = 2 + 15 - 7 \\
   \Rightarrow V = 17 - 7 \\
   = 10 \\
 $
$\therefore {\text{ }}$Option B is correct.

Note – In this type of question, we have to apply the Euler’s formula to find out the vertices of a pentagonal prism. Also, it is important to note that if we have to find out the edges and faces of a pentagonal prism in that case we have to use the same approach to get the required answer.