Question

A person is unable to see objects distinctly placed within \[50cm\] from his eyes.
$(A)$ Name the defect of vision the person is suffering from and list its two possible causes.
$(B)$ Draw a ray diagram to show the defect in the above case.
$(C)$ Mention the type of lens used by him for the correction of the defect and calculate its power. Assume that the near point for the normal eye is \[25cm\].
$(D)$ Draw a labeled diagram for the correction of the defect in the above case.

Answer 1

Hint: We know about four types of vision defects i.e. hypermetropia, myopia, presbyopia, and astigmatism. Two of the among are the problem of seeing an object in different places. Such as, for Hypermetropia we can’t see the nearer object, and for Myopia we can't see the far objects.
These two diseases happen for the small or big size of the eyeball than its natural size and also for the increase or the decrease of the focal length of the eye lenses. To calculate the power use the general lens equation and the relation between the power and the focal length.

Formula used:
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
Where $v = $ the image distance from the lens.
$u = $ the object distance from the lens.
$f = $ the focal length of the lens.
The power of the lens, $P = \dfrac{{100}}{f}$

Complete step by step solution:
A person is unable to see objects distinctly placed within \[50cm\] from his eyes.
$(A)$ if the eye can see the far object clearly but the nearer object blur – this defect is called Hypermetropia. In the above problem since the person is unable to see the objects that are placed within \[50cm\]. That means he can not see the nearer object. So the person is suffering from Hypermetropia which is also called Long Sight.
The two possible reasons for the defect is :
$1)$ The increase in the focal length of the eye lens from its natural length.
$2)$ The decrease in the size of the eyeball from its natural size.
$(B)$ The ray diagram of the Hypermetropia is shown below in the Fig-1:

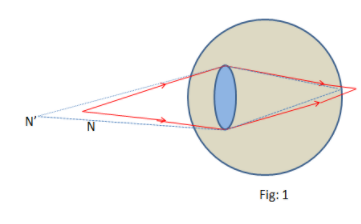
Let, the point $N$ is the nearer point of a normal eye (Fig-1). For the defect of the Long sight, the image of the object in the point $N$ will be created at the backside of the retina. Hence a person will not see clearly the object at the point $N$. In this case, the nearer point is situated at the point $N'$.

$(C)$ The defect can be removed by keeping a convex lens with a suitable focal length. The focal length should be such that the ray coming from the point $N$ seems to be coming from the point $N'$ after refracting in the convex lens. Hence, if the point $N$ is the object point then the point $N'$ be the virtual image by the convex lens.
From the lens equation $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$, we get
$\dfrac{1}{{ - d}} - \dfrac{1}{{ - D}} = \dfrac{1}{f}$
Where $v = $ the image distance from the lens $ = - d$
$u = $ the object distance from the lens $ = - D$
$f = $ the focal length of the lens.
Given, $D = 25$
$\therefore \dfrac{1}{f} = \dfrac{1}{D} - \dfrac{1}{d}$
$ \Rightarrow \dfrac{1}{f} = \dfrac{1}{{25}} - \dfrac{1}{d}$
$ \Rightarrow f = \dfrac{{25d}}{{d - 25}}$
Since, $d = 50 > 25,$
$\therefore f{\text{ positive}}$
The power of the convex lens,
$P = \dfrac{{100}}{f} = \dfrac{{100}}{{25d}}(d - 25)$
$ \Rightarrow P = (4 - \dfrac{{100}}{d})$
Since, $d = 50 > 25,$
$\therefore P{\text{ positive}}$

$(D)$ The labeled diagram for the correction of the Long sight defect:

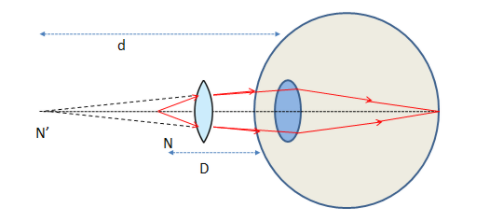
Note: The power of the convex lens is positive since the focal length is positive. Hence to correct the Hypermetropia or the Long sight defect a person should use the spectacles of a convex lens or we may say he should use spectacles of positive power.