Question

A person's eye level is $ 1.5{\text{ }}m $ . He stands in front of a $ 0.3{\text{ }}m $ long plane mirror which is $ 0.8{\text{ }}m $ above the ground. The height of the image he sees of himself is:
A) $ 1.5\,m $
B) $ 1.0\,m $
C) $ 0.8\,m $
D) $ 0.6\,m $

Answer 1

Hint : We will draw the ray diagram of the image seen by the person’s eye in the mirror. To find the height of the image, we will use relations between similar triangles that will be formed in the ray diagram.

Complete step by step answer
We’ve been given that a person whose eye level is at $ 1.5{\text{ }}m $ from the ground stands in front of a $ 0.3{\text{ }}m $ long plane mirror which is $ 0.8{\text{ }}m $ above the ground. Let’s draw a ray diagram for the situation:

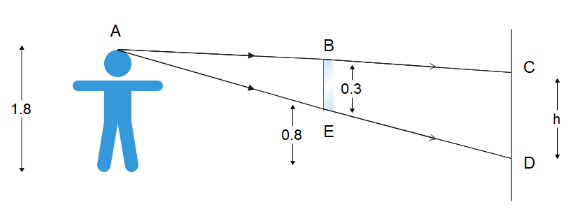
Since for a plane mirror, the object distance is the image distance, the distance between the object and the image will be $ 2x $ .
From the diagram, triangle ABE and ACD are similar triangles since all of their three sides are parallel to their counterparts.So, the ratio of the corresponding similar sides will be equal. So, we can write the ratio of the mirror height and the image height is equal to the ratio of the distance between the object and mirror distance and object and image distance, i.e.
 $\Rightarrow \dfrac{h}{{0.3}} = \dfrac{{2x}}{x} $
On cross multiplying the denominators and canceling with $ x $ on the right side, we can calculate the height of the image as:
 $\Rightarrow h = 0.6m $
Hence the height of the image will be $ h = 0.6m $ which corresponds to option (D).

Note
Here we have roughly taken that $ AB \approx x $ and $ AC \approx 2x $ however their lengths are actually a little longer. But this correction will be very negligible and we can ignore it to use the relation of similar triangles which will simplify the geometry of the situation very easily and we can hence find the height of the image.