Question

A person's eye level is 1.5m. He stands in front of a 0.3m long plane mirror which is 0.8m above the ground. The height of the image he sees of himself is:
A. 1.5m
B. 1.0m
C. 0.8m
D. 0.6m

Answer 1

Hint: Laws of reflection are to be put to use here. An object creates an image behind the mirror at the same distance that it has from the mirror in front of it. Properties of triangles are also required in these questions.

Formula used: Property of similar triangle:
Ratio of corresponding lengths are equal:
$\dfrac{AB}{AD} = \dfrac{BC}{DE}$

Complete step by step answer:
Consider a rough sketch of the situation that we have.

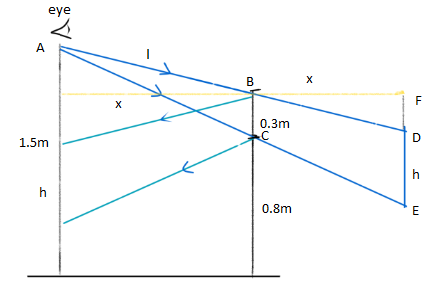
Let the person be standing in front of a mirror at a distance x. Behind the mirror, the image of the person will be at a distance of x.

Consider the triangles from the sketch:

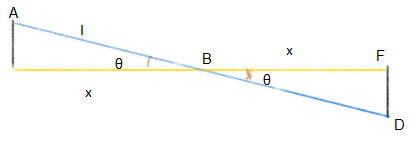
Both these right angled triangles have x and an angle $\theta$ and a right angle in common. This is quite sufficient for us to prove that both triangles have the remaining two edges (hypotenuse and perpendicular) equal.

Now, we are given that the length of the mirror is 0.3 m. This mirror is part of the triangle ABC and then we have another triangle behind it ADE. Now, if we compare the two triangles, we find them to be similar triangles (as the triangles have 3 angles that are equal). Thus, the ratio of the sides of the two triangles will be equal. We may write:
$\dfrac{AB}{AD} = \dfrac{BC}{DE}$
or, $\dfrac{l}{2l} = \dfrac{0.3m}{h}$
$h= 2 \times 0.3$ =0.6m
Therefore, we obtain the height of the image as h= 0.6m.

So, the correct answer is “Option D”.

Note: The angles and the corresponding lengths should be noted carefully in the similar triangles. One might make an error in choosing the sides of the similar triangles in the ratio so the calculations can differ.