Question

A physical balance has its arms of unequal length. A body weighs $18\;kg$ if kept in one pan and weighs $8\;kg$ if kept in the other pan. The true weight of the body is:
A. $13\;kg$
B. $12\;kg$
C. $10\;kg$
D. $16\;kg$

Answer 1

Hint: Try and recall how the physical balance works. That is, we know that to bring the balance to an equilibrium we need to place corresponding weights to stabilize it. To this end, use the principle of moments in each case to derive the clockwise and anticlockwise moments and arrive at the ratio of the arm lengths. Since this factor is common to measurements in both the cases, equate them, following which you will obtain the true weight of the body.

Formula used: Principle of moments: sum of clockwise moments = sum of anticlockwise moments
Moment = $F \times l $, where F is the applied force and l is the perpendicular distance from the pivot point.

Complete step by step answer:
Let us begin by first understanding how a physical balance works.
A physical balance is an instrument that is used to measure the mass or weight of an object accurate to its milligrams. It consists of two holders: One can hold the object whose mass is to be determined while the other holds the weights that are placed to balance out the mass of the object. Note that a physical balance usually comes with a weights box which usually contains weights ranging from the small to larger weights. At equilibrium the sum of the weights that are placed in the holder gives the weight of the object placed in the other holder.
A physical balance works on the principle of moments which suggests that when a system is balanced the total sum of the anti-clockwise moments will be equal to the sum of the clockwise moment. This means that when a system is stable or in balance, it is said to be in equilibrium as all the forces acting on the system cancel each other out. Keep this in mind for when we carry out our analysis.
A true balance, and hence a true weight, is measured by the physical balance when both arms of the balance are of equal lengths and both holders are of equal weights.
Our question states that arms of our physical balance are of unequal lengths. This means that the sum of weights that we place in the holder will not be equivalent to the true weight.
Let the arms of unequal length be $L_1$ and $L_2$ as shown in the diagram.
Let us now look at when the body is placed in holder A:
For the physical balance to achieve equilibrium, we are required to place weights totalling to $18\;kg$ in holder B.
The sum of clockwise moments will be: $W \times L_1$

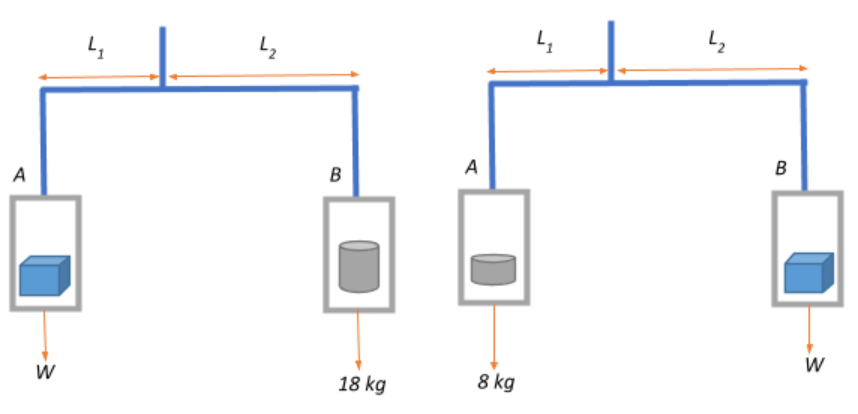
The sum of anticlockwise moments will be $18 \times L_2$
Therefore, at equilibrium, $ W \times L_1 = 18 \times L_2 \Rightarrow \dfrac{L_1}{L_2} = \dfrac{18}{W} $
Now let us look at when the body is placed in holder B:
For the physical balance to achieve equilibrium, we are required to place weights totalling to $8\;kg$ in holder A.
The sum of clockwise moments will be: $8 \times L_1$
The sum of anticlockwise moments will be $W\times L_2$
Therefore, at equilibrium, $ 8 \times L_1 = W\times L_2 \Rightarrow \dfrac{L_1}{L_2} = \dfrac{W}{8} $
Now, since the ratio $\dfrac{L_1}{L_2}$ will remain the same under both circumstances, we can equate the expressions that we got for them in both the cases, i.e., equating:
$\dfrac{18}{W} = \dfrac{W}{8} \Rightarrow W^2 = 18 \times 8 \Rightarrow W = \sqrt{144} \Rightarrow W=12\;kg $
Therefore, the true weight of the body is $12\;kg$

So, the correct answer is “Option B”.

Note: Notice that throughout the problem and even in the question the weight is given in kg. Physically, we usually treat weight as a force and express it as a factor of the acceleration due to gravity and in units of newton (N). It does not make any difference here as the g factor would get cancelled out since we are mostly dealing with linear relations and ratios, and this will not influence the final result that we get in any way. However, remember to always associate mass with g or kg units and weight with newton N units to maintain a consistent distinction between the two in case you are dealt with a problem where it actually matters.
Also remember that torque is the moment of force, so when there is a system that deals with torque, the two terms moment of force, and torque, can be interchangeably used.