Question

A pipe closed at one end produces a fundamental note of $412Hz$. It is cut into two pieces of equal length. The fundamental frequencies produced by the two pieces are:
$A)206Hz,412Hz$
$B)824Hz,1648Hz$
$C)412Hz,824Hz$
$D)206Hz,824Hz$

Answer 1

Hint: Fundamental note produced by a pipe is nothing but the first harmonic or the lowest frequency produced by the pipe. Fundamental frequency of a pipe is dependent on the openness as well as the closedness of the ends of the pipe used. It is also dependent on the length of the pipe and the speed of sound in air.
Formula used:
$1){{f}_{c}}=\dfrac{v}{4l}$
$2){{f}_{o}}=\dfrac{v}{2l}$

Complete answer:
Fundamental note produced by a pipe is nothing but the lowest frequency produced by the pipe, when the air column inside the pipe is made to start vibrating. It is also called a fundamental frequency or the first harmonic note produced by a pipe. This lowest frequency produced by a pipe is dependent on the nature of the pipe, length of the pipe and the speed of sound in air.
For a closed pipe, fundamental frequency is given by
 ${{f}_{c}}=\dfrac{v}{4l}$
where
${{f}_{c}}$ is the fundamental frequency produced by a closed pipe
$v$ is the speed of sound in air
$l$ is the length of the pipe
Let this be equation 1.
For an open pipe, fundamental frequency is given by
${{f}_{o}}=\dfrac{v}{2l}$
where
${{f}_{o}}$ is the fundamental frequency produced by an open pipe
$v$ is the speed of sound in air
$l$ is the length of the pipe
Let this be equation 2.
Here, by a closed pipe, we mean that the pipe has one of its ends closed while the other end is open. At the same time, by an open pipe, we mean that the pipe has both of its ends open.
Coming to our question, we are provided with a closed pipe of fundamental frequency $412Hz$. Let us call this closed pipe X.
Clearly, from equation 1, we have
${{f}_{c}}=\dfrac{v}{4l}\Rightarrow 412Hz=\dfrac{v}{4l}$
where
${{f}_{c}}=412Hz$ is the fundamental frequency produced by X
Let this be equation 3.
Now, it is said that this pipe (X) is cut into two pieces of equal length.
Therefore, one of the two pipes formed will be closed on one end while the other pipe will have both of its ends open, as shown in the following figure. Let us call these pipes Y and Z, such that Y is the closed pipe and Z is the open pipe, as shown below. It is also clear that the lengths of both these pipes (Y and Z) are the same and are equal to $\dfrac{l}{2}$.

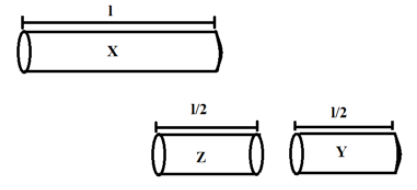
Let the fundamental frequency of Y be represented by ${{f}_{c1}}$. Using equation 1, ${{f}_{c1}}$ is given by
${{f}_{c1}}=\dfrac{v}{4\left( \dfrac{l}{2} \right)}=\dfrac{2v}{4l}=\dfrac{v}{2l}$
where
${{f}_{c1}}$ is the fundamental frequency produced by Y
$v$ is the speed of sound in air
$l$ is the length of X
Let this be equation 4.
Similarly, let the fundamental frequency produced by Z be represented by ${{f}_{o1}}$. Using equation 2, ${{f}_{o1}}$ is given by
${{f}_{o1}}=\dfrac{v}{2\left( \dfrac{l}{2} \right)}=\dfrac{2v}{2l}=\dfrac{v}{l}$
where
${{f}_{o1}}$ is the fundamental frequency produced by Z
$v$ is the speed of sound in air
$l$ is the length of X
Let this be equation 5.
Now, from equation 3, we know that
$\dfrac{v}{l}=4\times 412=1648Hz$
Substituting this value of $\dfrac{v}{l}$ in equation 4 and equation 5, we have
${{f}_{c1}}=\dfrac{v}{2l}=\dfrac{1648}{2}=824Hz$
and
${{f}_{o1}}=\dfrac{v}{l}=1648Hz$
where
${{f}_{c1}}$ and ${{f}_{o1}}$ are the frequencies produced by Y and Z, respectively

Therefore, the correct answer is option $B$.

Note:
Many musical instruments of wind type use the same principle of vibration of air column, as mentioned in the above solution. For example, different notes or sounds are produced in flutes and clarinets because the air columns inside these instruments are made to vibrate with different frequencies. The first harmonic note of a musical instrument is nothing but the lowest possible frequency produced by that instrument. This fundamental frequency of a musical instrument is dependent on the nature of the instrument, length of the instrument and the speed of sound in air.