Question

A pipe open at both ends has a fundamental frequency ‘f’ in air. The pipe is dipped vertically in water so that half of it is water. The fundamental frequency of the air column is now:
A. f/2
B. 3f/4
C. 2f
D. f

Answer 1

Hint: A transverse wave is the one which travels through a medium, making crests and troughs. Wave on a string is an example of a transverse wave. A longitudinal wave is the one which travels through the medium making compressions and rarefactions. Sound waves are an example of longitudinal waves. When two waves approach each other in the same place, on the same line, standing waves are formed. Organ pipe is an example of the situation in which standing waves are formed.

Complete answer:
Organ pipe is related to the experiments on sound waves. It is of two types. Open organ pipe is the one in which both ends are opened and then sound is passed through it. Closed organ pipe is the one in which only one end is open and the other is closed and then sound is passed.
Now, given: $f = \dfrac{\nu}{2L}$
But when the pipe is dipped in water to half of its length, the length of the pipe becomes halved and the pipe starts acting as closed organ pipe, having fundamental frequency $\nu = \dfrac{v}{4L}$ (Since water is a denser medium and sound will be reflected).

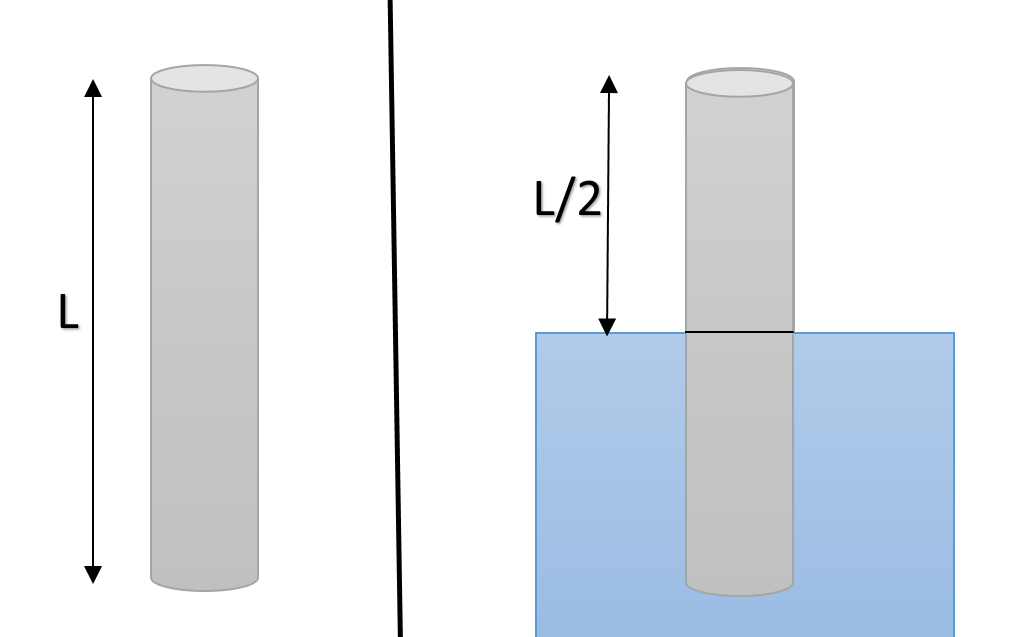
Hence $f^\prime = \dfrac{v}{4(L/2)} = \dfrac{v}{2L} = f$
Thus, there will be no technical difference between the fundamentals of pipe after being dipped into the water.

So, the correct answer is “Option D”.

Note:
Closed organ pipe is not really only that pipe which is blocked by a solid object at one end. It could be assumed closed id any medium denser than air is present on the other end. One must know that sound waves create standing waves inside the tube so that we can analyze the situation and know the parameters like frequency and conduct the experiment. Students are advised to derive these expressions once by their own.