Question

A plane glass mirror of thickness 3 cm of the material of $\mu ={\displaystyle \frac{3}{2}}$ is silvered on the back surface. When a point object is placed 9 cm from the front surface of the mirror, then the position of the brightest image from the front surface is
A. 9 cm
B.11 cm
C. 12 cm
D. 13 cm

Answer 1

Hint: In order to solve this problem we first need to draw the diagram and then we need to find the apparent height as the glass above the silver-coated film has the refractive index that is 1.5. So we need to find the apparent height by the suitable formula and then we have to find the point of the image formed according to the apparent height. Doing this gives you the right answers.

< b>complete step-by-step answer


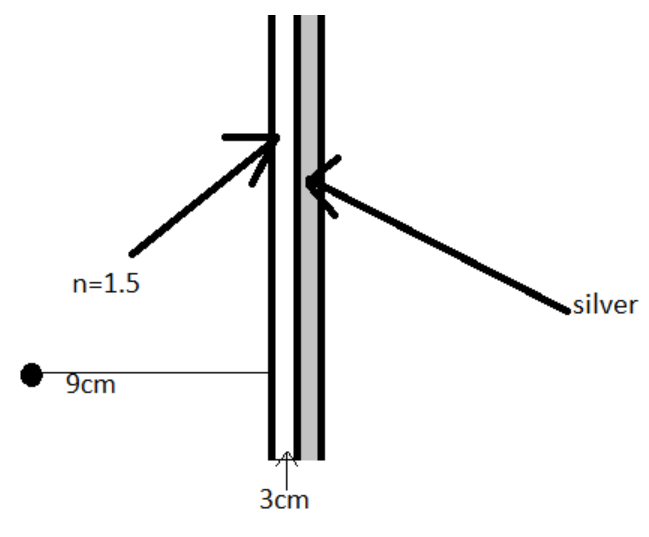
The above figure is the figure of the glass of refractive index 1.5 coated with the silver from the backside.
The object is 9 cm in front of the surface of the glass of the plane mirror and we know that the glass has a refractive index of 1.5 and of thickness 3cm.
So, the apparent height of the object from the mirror will be calculated after calculating the shift of the mirror.
Let the mirror be shifted x virtually because of the refractive index.
So,
$$\begin{gathered} \Rightarrow {\displaystyle \frac{\text{Real}\text{height}}{\text{apparent}\text{height}}}={\displaystyle \frac{3}{x}}=1.5 \\ \Rightarrow x=2cm \end{gathered}$$
So, the value of x is 2cm.
As we know that object distance is the same as that of image distance in the plane mirror, so we will add 2 twice with 9 to get the distance of the image that will be the same as the object distance from the virtual mirror.
So, we get the distance of the image as, $9+2+2=13\text{cm}$.
Hence, the image distance is $13\text{cm}$.
So, the correct option is D.

Note: When you get to solve such problems you always need to calculate the apparent distance of the image because of refractive index the image shifts itself and if the mirror is surfaced with a thick glass of refractive index then the mirror itself changes its position due to the refraction occurs and differ in the actual result due to refractive index then at that time the position of the image can be calculated b this method.