Question

A plano-convex lens, when silvered on the plane side, behaves like a concave mirror of focal length 60cm. However, when silver on the convex side, it behaves like a concave mirror of focal length 20cm. Then, the refractive index of the lens is:
A. 3.0
B. 1.5
C. 1.0
D. 2.0

Answer 1

Hint: We can consider the plano-convex lens with plane-side mirrored to act like two lenses. Use the formula for two consecutive lenses to find the effective focal length of the convex part. Then find the Radius of curvature using the second condition. Finally, use the focal length formula of the plano-convex lens to find the final result.

Formula Used:
The effective focal length of a plano-convex or plano-concave or similar mirrors is given by,
$\dfrac{1}{F}=\dfrac{2}{f}+\dfrac{1}{{{f}_{m}}}$.....................(1)

$f$ is the focal length of the first surface
${{f}_{m}}$ is the focal length of the mirrored surface
$F$ is the overall focal length

Focal length formula of the plano-convex lens is given by,
$\dfrac{1}{f}=(\mu -1)\dfrac{1}{R}$....................(2)

Where,
$\mu $ is the refractive index of the lens
$R$ is the Radius of curvature of the curved surface

Complete step-by-step answer:
First, let us look at the first configuration.

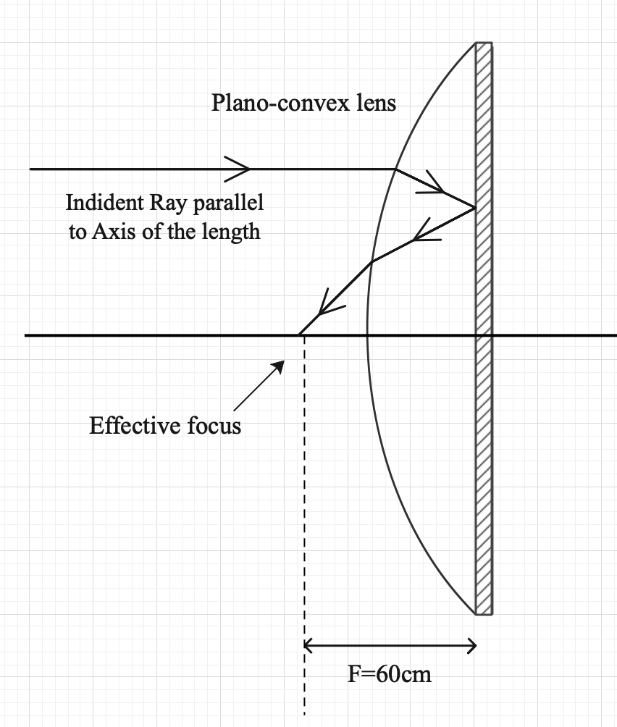
From equation (1) we can write that,
$\dfrac{1}{F}=\dfrac{2}{f}+\dfrac{1}{{{f}_{m}}}$
Given that,
$F=60$
${{f}_{m}}=\infty $ (because the plane surface is mirrored)

So, we write,
$\dfrac{1}{60}=\dfrac{2}{f}+\dfrac{1}{\infty }$
$\Rightarrow f=120$

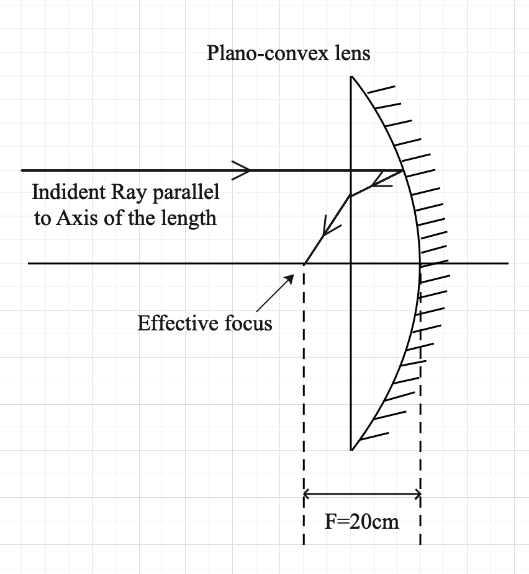
Now, for the second case,
$f=120$
Here, the convex side is mirrored, so
${{f}_{m}}=\dfrac{R}{2}$
And the overall system works like a concave mirror of focal length 20 cm.

Hence,$F=20$
So, we can write,
$\dfrac{1}{20}=\dfrac{2}{120}+\dfrac{2}{R}$
$\Rightarrow \dfrac{2}{R}=\dfrac{1}{20}-\dfrac{1}{60}$
$\Rightarrow R=60$
Hence, R =60cm

So, we can use equation (2) to find the refractive index of the lens. We can write,
$\dfrac{1}{f}=(\mu -1)\times \dfrac{1}{R}$
$\Rightarrow \dfrac{1}{120}=(\mu -1)\times \dfrac{1}{60}$
$\Rightarrow \dfrac{1}{2}=(\mu -1)$
$\Rightarrow \mu =1.5$
Hence, refractive index of the lens =1.5
So, the correct answer is - (B)

Note:
These equations should be memorized for accurate and fast solutions. However, you can follow the ray to find the image due to each refraction and reflection to find the focal length. However, that process is tough and time-consuming.