Question

A plot given shows P – T curves (where P is the pressure and T is the temperature) for two solvents X and Y, and isomolar solutions of NaCl in these solvents. NaCl completely dissociates in both the solvents. In addition to an equal number of moles of non-volatile solute S in equal amount (in Kg) of these solvents, the elevation of the boiling point of solvent X is three times that of solvent. Solute S is known to undergo dimerization in these solvents. If the degree of dimerization is 0.7 in solvent Y, the degree of dimerization in solvent X is:

Answer 1

Hint: The elevation in the boiling point is equal to the product of ionization of solute, molality, and molal elevation constant. The formula is $\Delta {{T}_{b}}=i\text{ x m x }{{\text{K}}_{b}}$. The value of i can be calculated by the reaction $2(S)\to {{S}_{2}}$.

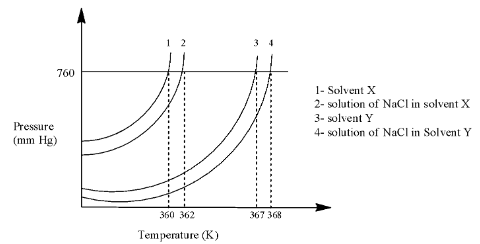
Complete answer: In the graph, there are four lines in which the first 2 lines are used for solvent X and the last two lines are used for solvent Y.
Line 2 is at 362 K and line 1 is at 360 K, so we can calculate the elevation in the boiling point as:
 $\Delta {{T}_{b(X)}}=362-360=2$
Line 4 is at 368 K and line 3 is at 367 K, so we can calculate the elevation in the boiling point as:
$\Delta {{T}_{b(Y)}}=368-367=1$
According to the formula, we can write for X and Y as:
$\Delta {{T}_{b(X)}}=i\text{ x }{{\text{m}}_{NaCl}}\text{ x }{{\text{K}}_{b(X)}}$
$\Delta {{T}_{b(Y)}}=i\text{ x }{{\text{m}}_{NaCl}}\text{ x }{{\text{K}}_{b(Y)}}$
When we divide the above equations, we get:
$\dfrac{{{K}_{b(X)}}}{{{K}_{b(Y)}}}=2$
Since the dimerization takes place, we can write the equation as:
$2(S)\to {{S}_{2}}$
After the equilibrium is attained, the concentration of S will be $1-\alpha $ and the value of ${{S}_{2}}$ will be $\dfrac{\alpha }{2}$
So, the value of i, will be:
$i=(1-\dfrac{\alpha }{2})$
Now, putting these values in the elevation in boiling point equation, we get:
$\Delta {{T}_{b(X)}}=(1-\dfrac{{{\alpha }_{1}}}{2})\text{ x }{{\text{m}}_{NaCl}}\text{ x }{{\text{K}}_{b(X)}}$
$\Delta {{T}_{b(Y)}}=(1-\dfrac{{{\alpha }_{2}}}{2})\text{ x }{{\text{m}}_{NaCl}}\text{ x }{{\text{K}}_{b(Y)}}$
In the question, it is given that:
$\Delta {{T}_{b(X)}}=3\text{ x }\Delta {{T}_{b(Y)}}$
Combining, all these we can write:
$(1-\dfrac{{{\alpha }_{1}}}{2})\text{ x }{{\text{K}}_{b(X)}}=3\text{ x }(1-\dfrac{{{\alpha }_{2}}}{2})\text{ x }{{\text{K}}_{b(X)}}$
$2\text{ x }(1-\dfrac{{{\alpha }_{1}}}{2})=3\text{ x }(1-\dfrac{{{\alpha }_{2}}}{2})$
${{a}_{2}}$ = 0.7 and ${{a}_{1}}$ = 0.05.
The degree of dimerization of solvent X is 0.05.

Note: Don’t get confused between the formulas $\Delta {{T}_{b}}=i\text{ x m x }{{\text{K}}_{b}}$ and $\Delta {{T}_{b}}=\text{ m x }{{\text{K}}_{b}}$, the former is used when there is any electrolyte or ionic compound is present in the solution and the latter is used when covalent compound is present.