Question

A plot of land has a shape of a parallelogram. It is to be covered by mud. Find the cost of spreading mud at the rate Rs. $100$ per square metre while the adjacent side of the plot are $39$ m and $25$ m metre and the diagonal is $56$ m.​

Answer 1

Hint: We will first start by drawing a figure of the parallelogram along with its dimensions and then we will start by applying the property of parallelogram that the diagonal bisects it into two congruent triangle therefore we will find the area of one triangle using the formula: $\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}$ , where $S=\dfrac{a+b+c}{2}$ and $a,b,c$ are the sides of triangle, then we will multiply it by 2 in order to get the area of the whole parallelogram. Finally, we will multiply the obtained area into 100 to get the total cost of spreading mud.

Complete step by step answer:
It is given that the land is in the shape of a parallelogram. So, first let’s draw the figure of the plot of land using the dimensions given in the question:

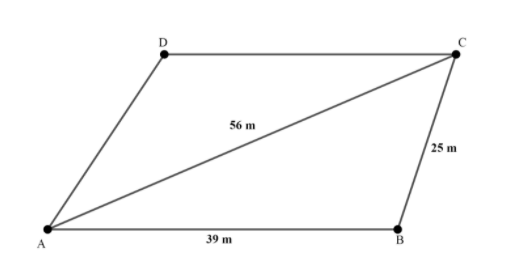
As we know that the opposite sides of parallelogram are equal so, we have:
$AB=CD=39\text{ m}$and $BC=AD=25\text{ m}$.
And we have a diagonal: $AC=56\text{ m}$
According to the properties of a parallelogram, we know that the diagonal of a parallelogram bisects the parallelogram into two congruent triangles, therefore we will get:
Area of parallelogram = \[Ar\left( \Delta ABC \right)+Ar\left( \Delta ADC \right)=2\times Ar\left( \Delta ABC \right)\text{ }......\text{ Equation 1}\text{.}\]
Now we know that the formula for the area of triangle = $\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}$ , where $S=\dfrac{a+b+c}{2}$ and $a,b,c$ are the sides of triangle.
Now, taking the \[\Delta ABC\], we have : $AB=a=39\text{ m, }BC=b=25\text{ m, }AC=c=56\text{ m}$ .
And therefore, $S=\dfrac{a+b+c}{2}=\dfrac{39+25+56}{2}=\dfrac{120}{2}=60$ , Putting all these values in the formula for the area of the triangle, we will have:
\[\begin{align}
  & Ar\left( \Delta ABC \right)=\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\Rightarrow Ar\left( \Delta ABC \right)=\sqrt{60\left( 60-39 \right)\left( 60-25 \right)\left( 60-56 \right)} \\
 & Ar\left( \Delta ABC \right)=\sqrt{60\left( 21 \right)\left( 35 \right)\left( 4 \right)} \\
 & Ar\left( \Delta ABC \right)=\sqrt{5\times 2\times 3\times 2\times 7\times 3\times 7\times 5\times 2\times 2} \\
 & Ar\left( \Delta ABC \right)=\left( 5\times 2\times 3\times 7\times 2 \right) \\
 & Ar\left( \Delta ABC \right)=420\text{ }{{\text{m}}^{2}} \\
\end{align}\]
Putting this value in equation 1 we will have: Area of the parallelogram $ABCD$ = \[2\times Ar\left( \Delta ABC \right)\]
Therefore, Area of the parallelogram $ABCD$ = $2\times 420=840\text{ }{{\text{m}}^{2}}$
It is given that the cost of spreading the mud is Rs. $100$ per square metre. Thus the total cost of spreading across the entire parallelogram shaped plot will be: $100\times 840=84000\Rightarrow \text{ Rs}\text{. }84000$

So, the correct answer is RS. 84000.

Note: Since the properties of a parallelogram plays an important part in these types of questions. You must know the important properties, there are 6 important properties of a parallelogram :
A. Opposite sides are congruent. (AB=CD)
B. Opposite angles are congruent (D = B).
C. Consecutive angles are supplementary $\left( A+D \right)={{180}^{\circ }}$
D. If one angle is right, then all angles are right.
E. The diagonals of a parallelogram bisect each other.
F. Each diagonal of a parallelogram separates it into two congruent triangles.