Question

A point object is situated at a distance of 36cm from the center of the sphere of radius 12cm and refractive index 1.5. Locate the position of the image due to refraction through the sphere.
A. 24cm from the surface
B. 36cm from the centre
C. 24cm from the centre
D. 18cm from the centre

Answer 1

Hint As known when passing through a curved surface having some different refractive index then refraction occurs. Using the relation when we travel from one medium to another through a curved surface and position of object and radius of the curved surface is given. Use the same relation to find the position of the image.



Complete step-by-step solution:
  In the given question:
Object is located at distance 36cm from centre; \[u = - 36\] (negative because of sign convention)
Refractive index of outside medium is \[{n_1} = 1\]
Refractive index of sphere is \[{n_2} = 1.5\]
The given situation can be described as below:

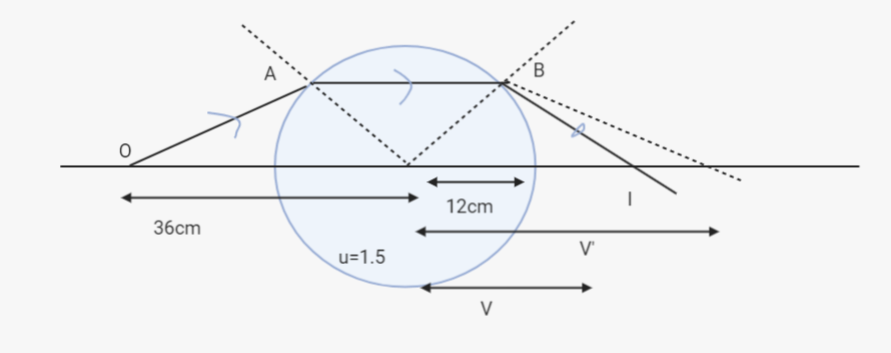
What is a refraction of O at A produces a virtual image then that virtual image again acts as a virtual object at B. Now this virtual object produces a real image at point I.
Using relation:
\[\dfrac{{{n_1}}}{v} - \dfrac{{{n_2}}}{u} = \dfrac{{({n_1} - {n_2})}}{R}\]
Where:
Putting given values:
\[\dfrac{{1.5}}{{v'}} - \dfrac{1}{{ - 36}} = \dfrac{{1.5 - 1}}{{12}}\]
On solving we get:
\[v' = 108cm\]
Now this virtual image will act as a virtual object to form the real image.
\[u\] will be now \[v'\]
So the modified formula is:
\[\dfrac{{{n_1}}}{v} - \dfrac{{{n_2}}}{{v'}} = \dfrac{{({n_1} - {n_2})}}{R}\]
Putting values:
\[\dfrac{1}{v} = \dfrac{{1.5}}{{108}} = \dfrac{{1 - 1.5}}{{ - 12}}\]
On solving we get:
\[v = 18cm\]
So the final image will be formed at 18cm from the centre as shown in figure.
Hence option D is correct.


Note:-
The main reason why the light changes its direction while travelling from one medium to another depends on the factor known as the Refractive Index of the Material. As the refractive index is different for different mediums, thus the speed of the light changes while travelling through them, resulting in the change of direction.