Question

A point P moves so that its perpendicular distance from two given lines $AB$ and $CD$ equal. State the locus of the point $P$.

Answer 1

Hint:Try to imagine the way $P$ will move, and it will be easy for you to find the locus when the lines given are parallel to each other, but for the case where the lines don’t intersect, imagine the point to be originally kept at their intersection, and then try moving it in such a way, so that its perpendicular distance from both the lines is equal.

Complete step-by-step answer:
Now let’s try imagining the condition. For that, first we’ll consider the case where the lines given are parallel to each other and never intersect. Now, for the point to be equidistant from both the lines, it is necessary that it remains so at each point of its locus. So, we can assume two perpendicularly opposite points on the two parallel lines. Now, we need to find another point between these two assumed points, that is equidistant to them both, and this will be none other than the two points’ midpoint. Therefore, if we go on extrapolating the individual midpoints of each pair of opposite points that we assume on the parallel lines, we’ll ultimately arrive at a straight line, that is midway between the two lines, and is parallel to them both.
Thus, when two lines $AB$ and $CD$ are parallel, then the locus of the point $P$ which is equidistant from $AB$ and $CD$ is a line $L$ in the midway of $AB$ and $CD$ and is parallel to them.

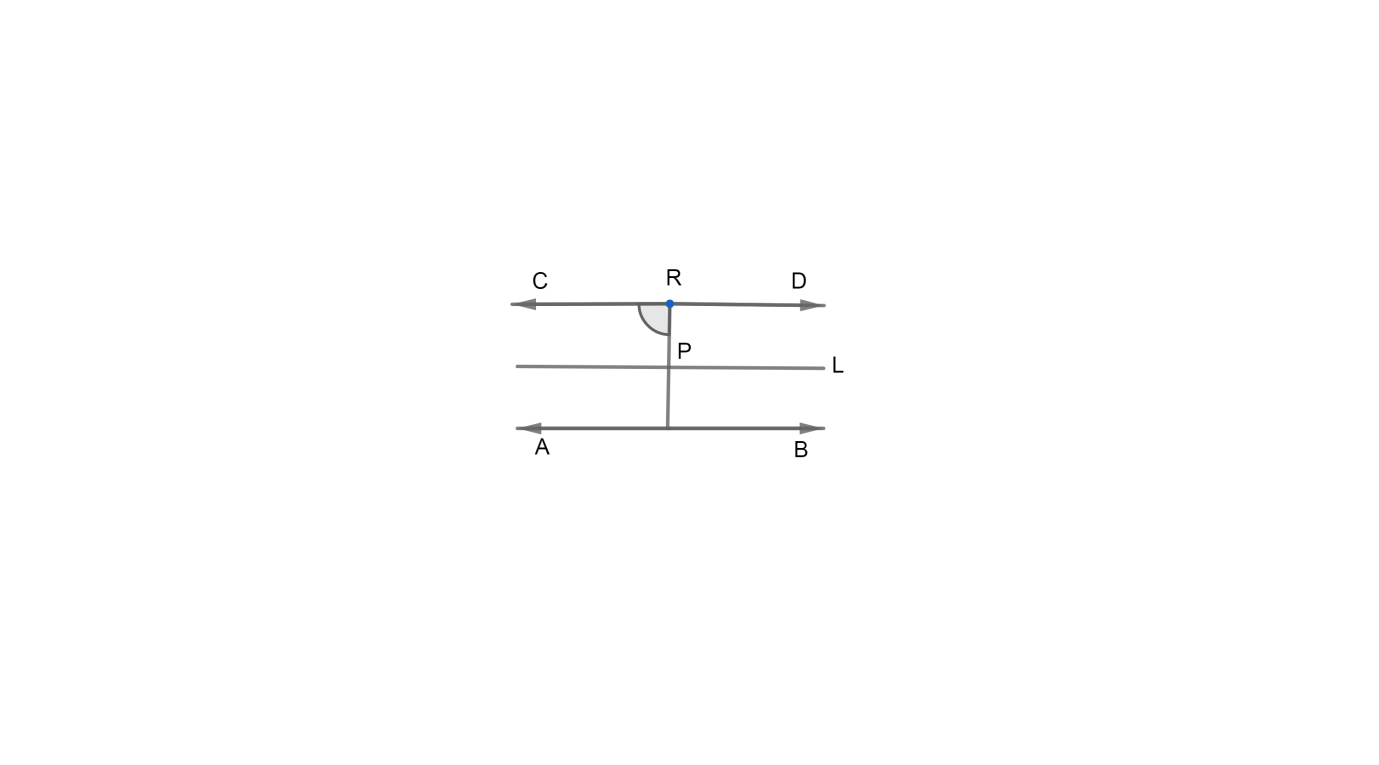
Now, let’s imagine the condition where the lines given are intersecting. For this, let’s assume the case where the point is equidistant to both the lines, and the distance is zero. This is possible only in one condition, when the point lies at the intersection of the two lines. Hence, one point in the locus of the point will actually be the intersection point of the two lines. Now, try imagining what will happen if we move along the angle bisector of the angle formed by the intersecting lines. Below is a figure to aid you in imagining.
If $AB$ and $CD$ are intersecting lines, then the locus of the point $P$ will be a pair of the straight lines $l$ and $m$ which bisect the angles between the given lines $AB$ and $CD$.

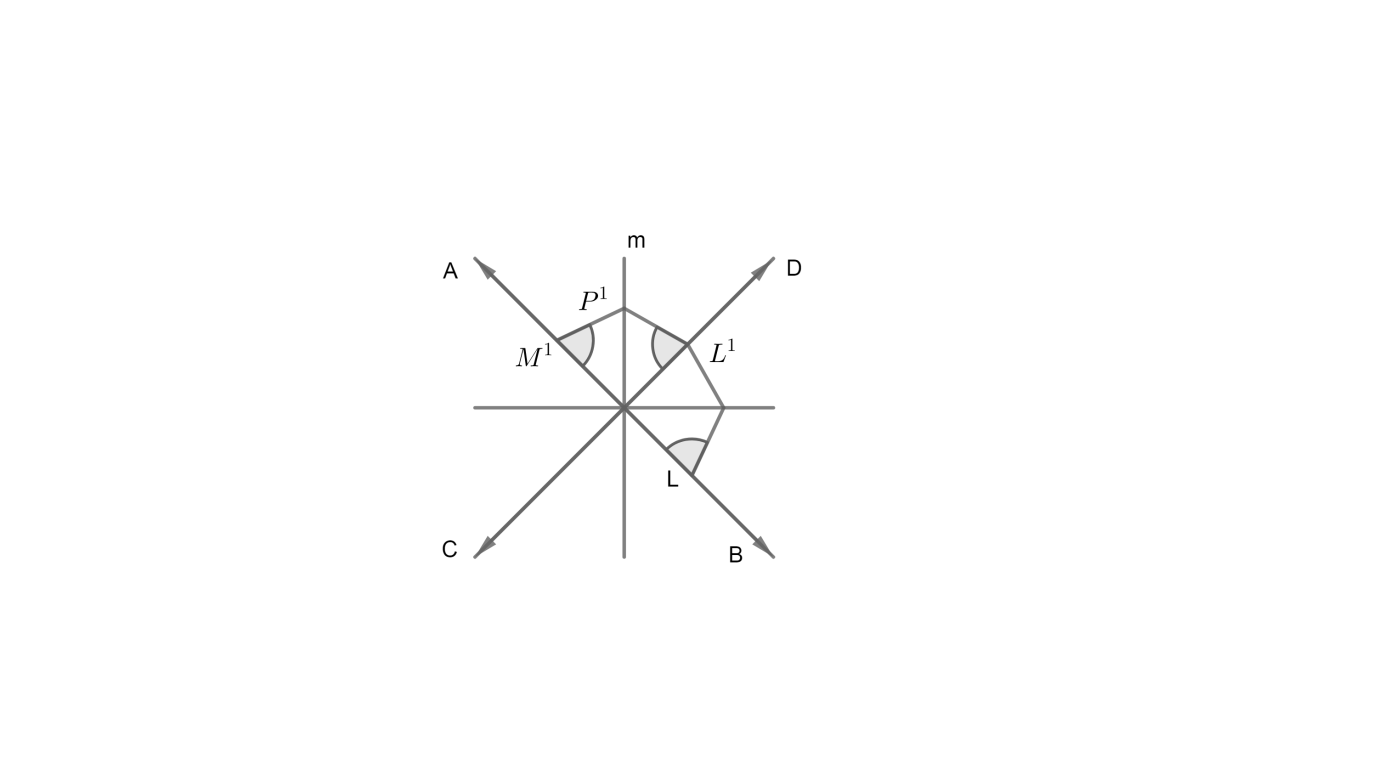
Thus, the locus of point $P$ will be the line $L$ as shown if the lines $AB$ and $CD$ are parallel, and the locus will be the angle bisector of the angle formed by the lines, if the lines are not parallel.

Note: Most of the students often misunderstand the concept of \[{{\bot }^{rl}}\] distance from two given lines i.e. equal. It means that the distance of the point from the two lines has to be equal at any given instant, it doesn’t have to remain constant all through the locus, because then the locus will simply be a point. So, don’t confuse yourself.