Question

A potentiometer circuit has been set up for finding the internal resistance of a given cell. The main battery, used across the potentiometer wire, has an emf of 2V and a negligible internal resistance. The potentiometer wire itself is 4m long. When the resistance, R, connected across the given cell, has values of (i) infinity (ii) 9.5$\Omega $, the balancing lengths on the potentiometer wire are found to be 3m and 2.85m respectively. The value of internal resistance of the cell is
$\text{A}\text{. }0.25\Omega $
$\text{B}\text{. }0.95\Omega $
$\text{C}\text{. }0.5\Omega $
$\text{D}\text{. }0.75\Omega $

Answer 1

Hint: The ratio of the potential difference across both the shunt resistances is equal to the ratio of the respective balancing lengths, i.e. $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$. The potential difference across a shunt resistance R is $V=\dfrac{ER}{(r+R)}$. Use these formulas to find the internal resistance of the cell.
Formula used:
$V=iR$

Complete step-by-step solution
Let us first understand the working of a potentiometer. To understand better, follow the given figure. This given figure is a simple setup of a potentiometer when it is used to measure the internal resistance of the unknown cell.

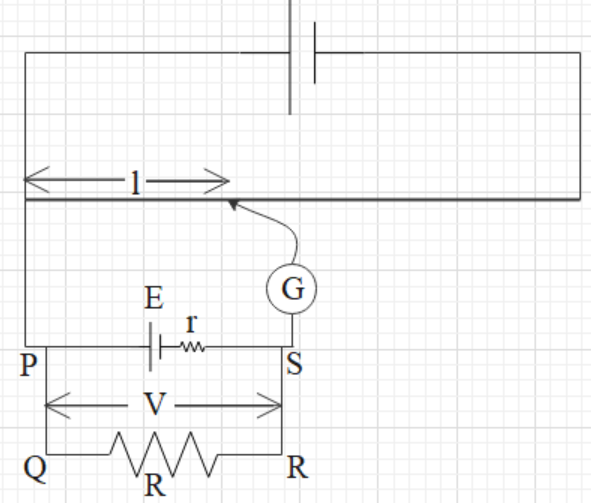
A potentiometer consists of a long wire of some known resistance and its total length is L (AB). It is connected to a cell and a potential difference is created across the wire.
J is a moveable point to find the balancing length. When there is zero current found in the galvanometer, the circuit is balanced.
When the circuit is balanced, the voltage (V) across the shunted resistance (R) is directly proportional to the balancing length (l) i.e. $V\propto l$.
Therefore, V=kl, where k is a constant.
When the circuit is balanced, $V=E-ir$ and V=iR, where i is the current in the circuit PQRS and r is the internal resistance of the cell (E).
This implies that E - ir = iR.
$\Rightarrow E=i(r+R)\Rightarrow i=\dfrac{E}{(r+R)}$.
Therefore,
$\Rightarrow V=E-ir=E-\left( \dfrac{E}{(r+R)} \right)r$
$\Rightarrow V=E\left( 1-\dfrac{r}{(r+R)} \right)$
$\Rightarrow V=\dfrac{ER}{(r+R)}$
Now, divide the numerator and the denominator by R.
$\Rightarrow V=\dfrac{\dfrac{ER}{R}}{\dfrac{(r+R)}{R}}=\dfrac{E}{\dfrac{r}{R}+1}$
When a resistance of infinity, let the voltage across the resistance be ${{V}_{1}}$ and the balancing length be ${{l}_{1}}$.
Therefore, ${{V}_{1}}=k{{l}_{1}}$ …. (i).
And ${{V}_{1}}=\dfrac{E}{\dfrac{r}{R}+1}$.
But, if $R\to \infty $ then $\dfrac{r}{R}\to 0$.
$\Rightarrow {{V}_{1}}=\dfrac{E}{0+1}=E$ …. (ii).
Let the voltage across the shunted resistance of 9.5$\Omega $ be ${{V}_{2}}$ and the balancing length be ${{l}_{2}}$.
Therefore, ${{V}_{2}}=k{{l}_{2}}$ …. (iii).
And ${{V}_{2}}=\dfrac{9.5E}{(r+9.5)}$ ….. (iv).
Divide equations (i) and (iii).
$\Rightarrow \dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{{{l}_{1}}}{{{l}_{2}}}$.
Here, ${{l}_{1}}$= 3cm and ${{l}_{2}}$= 2.85cm.
This gives us that
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Now, divide equations (ii) and (iv).
$\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{E}{\dfrac{9.5E}{(r+9.5)}}=\dfrac{(r+9.5)}{9.5}$
But $\dfrac{{{V}_{1}}}{{{V}_{2}}}=\dfrac{3}{2.85}$.
Therefore,
$\dfrac{(r+9.5)}{9.5}=\dfrac{3}{2.85}$
$\Rightarrow 2.85(r+9.5)=3(9.5)$
$\Rightarrow 2.85r+27.075=28.5$
$\Rightarrow r=\dfrac{28.5-27.075}{2.85}=\dfrac{1.425}{2.85}=0.5\Omega $
Therefore, the internal resistance of the given cell is $0.5\Omega $
Hence, the correct option is C.

Note: Note that the emf of the unknown cell must always be less than the emf of the main cell. If the emf of the cell that is to be measured is more than the emf of the main cell, then the balancing length will be more than the length of the resistance wire and we will not be able to measure the emf of the cell.