Question

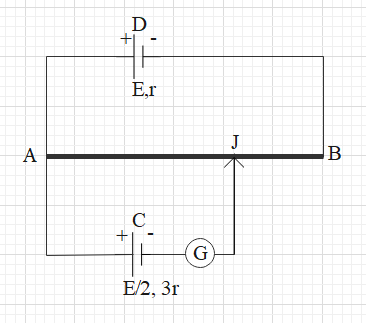
A potentiometer wire AB having length L and resistance 12r is joined to a cell of emf E and internal resistance r. A cell C having emf $\dfrac{E}{2}$ and internal resistance 3r is connected. The length AJ at which the galvanometer is shown in fig. show no deflection is

$\text{A}\text{. }\dfrac{5}{12}L$
$\text{B}\text{. }\dfrac{11}{24}L$
$\text{C}\text{. }\dfrac{11}{12}L$
$\text{D}\text{. }\dfrac{13}{24}L$

Answer 1

Hint: When the galvanometer shows no deflection, there is zero current in the galvanometer. This happens when the potential difference and emf of an unknown cell are equal. Using V=iR, find the current in the loop ABD and then the value of resistance across AJ in terms of r. Later, use $R=\dfrac{\rho l}{A}$ and find the relation between length AJ and L.
Formula used:
V=iR
$R=\dfrac{\rho l}{A}$

Complete step by step solution:
A potentiometer is a device that is used to measure the emf of an unknown cell. You can see a simple setup of a potentiometer in the figure given in the question.
 We know that a cell creates a potential difference across a wire or a resistor. And due to resistance of the wire, there is a flow of charges and we say that there is a current in the circuit.
Therefore, there will be some current in the given circuit. A galvanometer is a device used to detect current in the circuit. Hence, if a current is flowing through the galvanometer, it will show some readings.
When the galvanometer shows no deflection or zero reading, there is no current flowing through the galvanometer. We say that the circuit is balanced and the length AJ is called balancing length. This is possible when the potential difference across the AJ is equal to the emf of the cell C.
Let the potential difference across AJ be V.
Hence, $V=\dfrac{E}{2}$
There will be a current in the loop consisting points A, B and D. Let that current be i. The total resistance in the loop is 12r+r = 13r. From Ohm’s law, we know V=iR. Hence, E=i(13r).
$\Rightarrow i=\dfrac{E}{13r}$.
Let the balancing length (AJ) be l and resistance of AJ be R’.
The potential difference across AJ is $V=\dfrac{E}{2}$. The current in AJ is $i=\dfrac{E}{13r}$.
Hence, V=iR’
$\Rightarrow \dfrac{E}{2}=\left( \dfrac{E}{13r} \right)R'$
$\Rightarrow \dfrac{1}{2}=\dfrac{R'}{13r}$
$\Rightarrow R'=\dfrac{13r}{2}$
The cross sectional area of wire AB be uniform and be A. Let its resistivity be $\rho $.
Therefore, $R'=\dfrac{\rho l}{A}$ ….. (i)
And
$12r=\dfrac{\rho L}{A}$ ….. (ii)
Divide equation (i) and equation (ii).
$\Rightarrow \dfrac{R'}{12r}=\dfrac{\dfrac{\rho l}{A}}{\dfrac{\rho L}{A}}$
$\Rightarrow \dfrac{R'}{12r}=\dfrac{l}{L}$
$\Rightarrow R'=\dfrac{12rl}{L}$
And we found that $R'=\dfrac{13r}{2}$
This means that $\dfrac{13r}{2}=\dfrac{12rl}{L}$
$\Rightarrow l=\dfrac{13L}{24}$
The balancing length is $\dfrac{13L}{24}$,
Hence, the correct option is D.

Note: Note that the emf of the unknown cell (i.e C) must be less than the emf of the main cell (D). Otherwise, we will not find a balancing length.
The emf of the unknown cell is given by $E=\dfrac{Vl}{L}$, where V is the potential difference across the resistance wire (AB).
The drawback of this method is that we cannot find the internal resistance of the unknown cell.