Question

A prism having an apex angle of 4˚ and refractive index of 1.50 is located in front of a virtual plain mirror as shown in the figure. A horizontal ray of light is incident on the prism. The total angle through which the ray is deviated is?

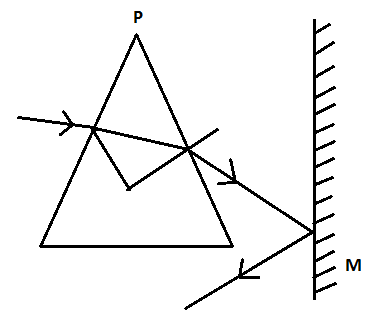
                  Figure (1)

A. $4{}^\circ $ clockwise
B. $178{}^\circ $ clockwise
C. $2{}^\circ $ clockwise
D. $8{}^\circ $ clockwise

Answer 1

Hint: here due to two optical objects we have to use a combination of two concepts. One is the angle of deviation by prism and second is the reflection of light by a pain mirror. When light passes through prism it undergoes refraction. Once the refracted light falls over the plain mirror at a certain angle it gets reflected by the same angle of incidence.
As per the given data,
Apex angle (A) =$4{}^\circ $
Refractive index of prism (u) =1.50

Formula to be used:
Deviation angle of prism $\left (\delta\right )= \left ( u-1 \right )\times A$
Relation between incident angle and reflection angle in case of plain mirror: $\angle i=\angle r$

Complete answer:
So as a prism is 3D objects by which a ray goes into refraction. The angle by which the ray will deviate from its path by refraction depends on two factors one is the refractive index and second is the apex angle of the prism.
 For better explanation we can re-draw the given diagram(figure (1)) as figure(2)

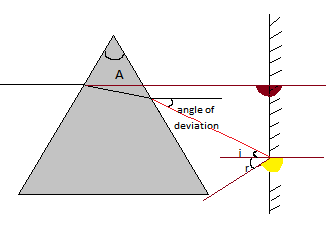
                        Figure (2)

Mathematically:
Deviation angle of prism is given by
 $\left (\delta\right )= \left ( u-1 \right )\times A$
By putting the provided data:
Deviation angle of prism
$\left (\delta\right )= \left ( 1.5-1 \right )\times 4$
\[\left (\delta\right )= \left ( 0.5 \right )\times 4\]
\[\left( \delta \right)=2{}^\circ \]
Now by looking at the figure angle of deviation through the prism would be the incidence angle for the plain mirror.
(i.e. basic geometrical relation)
$\delta =\angle i$
From Law of reflection of plain mirror we can conclude that:
$\angle i=\angle r=2{}^\circ $
So the angle of deviation of the ray after passing through the whole setup which is shown is the above figure from the clockwise direction (highlighted in yellow colour in the figure) would be:
(180 - 2) = 178˚ clockwise.

So, the correct option for the question will be option B. 178˚ clockwise.

Note:
Read the question carefully and go through the diagram. Just keep that in mind that the deviation of angle is asked for the whole set up and not for the prism. As all the options are for clockwise angle of deviation so don’t forget to calculate that.