Answer
463.8k+ views
Hint: First, we will use the tangents drawn from an exterior point to a circle are equal in length and then add the obtained equations. Then we will use the \[AP + BP = AB\], \[BQ + CQ = BC\], \[CR + DR = CD\] and \[AS + DS = AD\] to simplify this expression.
Complete step by step answer:
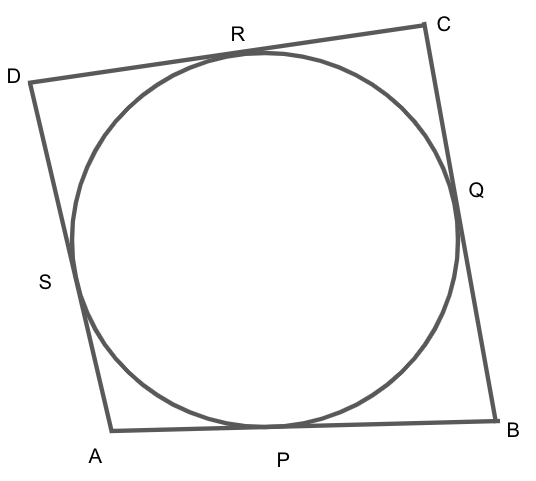
We are given that a quadrilateral ABCD is drawn to circumscribe a circle.
We know that tangents drawn from an exterior point to a circle are equal in length, so we have
\[ \Rightarrow AP = AS{\text{ ......eq.(1)}}\]
\[ \Rightarrow BP = BQ{\text{ ......eq.(2)}}\]
\[ \Rightarrow CR = CQ{\text{ ......eq.(3)}}\]
\[ \Rightarrow DR = DS{\text{ ......eq.(4)}}\]
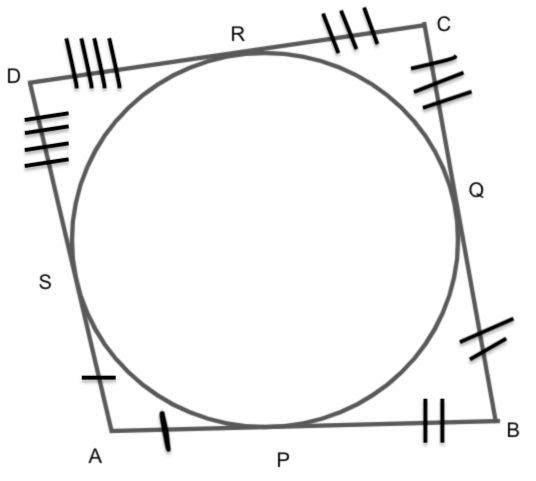
Adding the equations (1), (2), (3) and (4), we get
\[ \Rightarrow AP + BP + CR + DR = AS + BQ + CQ + DS\]
Rewriting the above equation, we get
\[ \Rightarrow \left( {AP + BP} \right) + \left( {CR + DR} \right) = \left( {AS + DS} \right) + \left( {BQ + CQ} \right){\text{ .......eq.(5)}}\]
Since we also know that AB is a line segments and when any point P cuts this line segments, then \[AP + BP = AB\].
From the same procedure, we get
\[BQ + CQ = BC\]
\[CR + DR = CD\]
\[AS + DS = AD\]
Using these sums from the given diagram in the equation (5), we get
\[ \Rightarrow AB + CD = AD + BC\]
Hence, proved.
Note: In this question, we know that circumscribes a circle is to draw on the outside of just touching the corner points but never crossing. Here a quadrilateral is circumscribed around a circle. Students must crack the point of using that tangents drawn from an exterior point to a circle are equal in length. If we are able to crack this point, then the proof is very simple.
Complete step by step answer:
We are given that a quadrilateral ABCD is drawn to circumscribe a circle.
We know that tangents drawn from an exterior point to a circle are equal in length, so we have
\[ \Rightarrow AP = AS{\text{ ......eq.(1)}}\]
\[ \Rightarrow BP = BQ{\text{ ......eq.(2)}}\]
\[ \Rightarrow CR = CQ{\text{ ......eq.(3)}}\]
\[ \Rightarrow DR = DS{\text{ ......eq.(4)}}\]

Adding the equations (1), (2), (3) and (4), we get
\[ \Rightarrow AP + BP + CR + DR = AS + BQ + CQ + DS\]
Rewriting the above equation, we get
\[ \Rightarrow \left( {AP + BP} \right) + \left( {CR + DR} \right) = \left( {AS + DS} \right) + \left( {BQ + CQ} \right){\text{ .......eq.(5)}}\]
Since we also know that AB is a line segments and when any point P cuts this line segments, then \[AP + BP = AB\].
From the same procedure, we get
\[BQ + CQ = BC\]
\[CR + DR = CD\]
\[AS + DS = AD\]
Using these sums from the given diagram in the equation (5), we get
\[ \Rightarrow AB + CD = AD + BC\]
Hence, proved.
Note: In this question, we know that circumscribes a circle is to draw on the outside of just touching the corner points but never crossing. Here a quadrilateral is circumscribed around a circle. Students must crack the point of using that tangents drawn from an exterior point to a circle are equal in length. If we are able to crack this point, then the proof is very simple.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

If the coordinates of the points A B and C be 443 23 class 10 maths JEE_Main

If the mean of the set of numbers x1x2xn is bar x then class 10 maths JEE_Main

What is the meaning of celestial class 10 social science CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE