Question

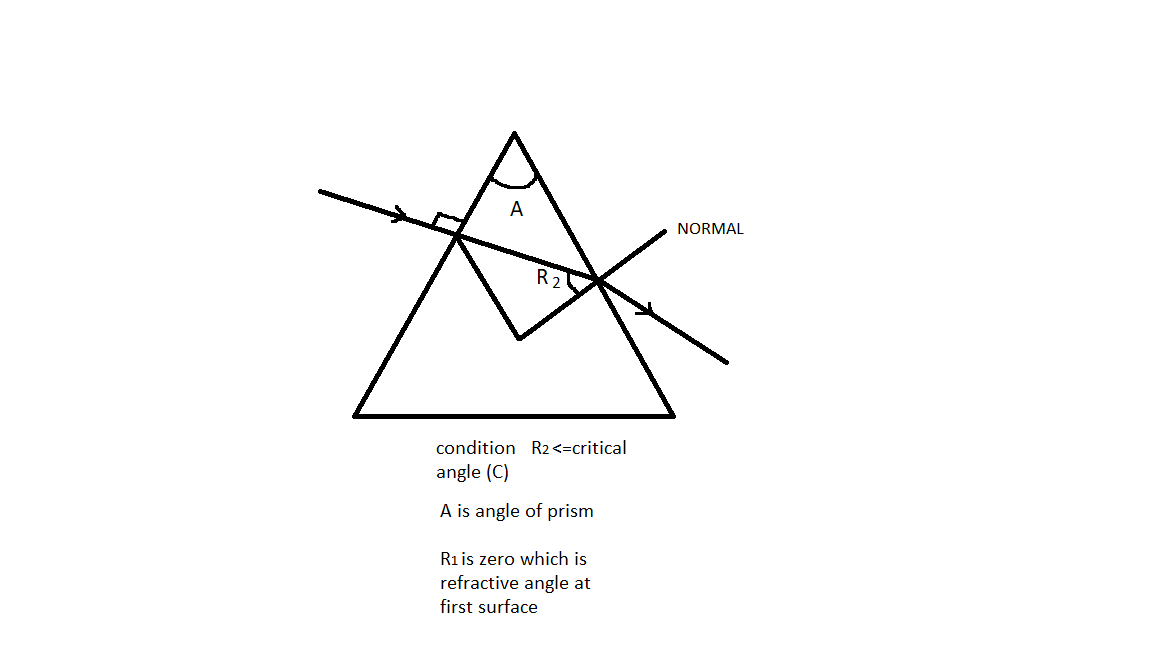
A ray of light incident normally on the first face of prism of refracting angle A and critical angle C. the ray emerges from the second face of the prism when following condition satisfies:
A.$C>\,A$
B.$C$
C.$C\ge A$
D.$C\le A$

Answer 1

Hint:Refraction from surfaces of prism concept to be used here.
On the first surface it is a normal incident so the incident and refracted angle at the first surface is zero.
From the equation $A={{R}_{1}}+{{R}_{2}}$, where $A$ is the angle of prism and ${{R}_{1}}$, ${{R}_{2}}$ are refractive angle at first surface and incident angle at second surface, find ${{R}_{2}}$.
And apply the condition for the critical angle at the second surface to find the condition for emerging from the second surface.

Complete answer:
Critical angle is that incident angle for which refractive angle is ${{90}^{o}}$
$\theta ={{\sin }^{-1}}\left( \dfrac{{{n}_{2}}}{{{n}_{1}}} \right)$
In our case for the first surface incident and refracted angle are ${{0}^{o}}$
For the rays to come out of any surface the incident angle must be less than the critical angle for the interface
For the first surface in the figure of the prism incident angle and refractive angle both are ${{0}^{o}}$.
So ${{R}_{1}}=0$
Now the ray passes without refraction to the second surface and strikes with an incident angle${{R}_{2}}$
From $\left( 1 \right)$
$\Rightarrow A={{R}_{1}}+{{R}_{2}}$
$\Rightarrow A={{R}_{2}}.......\left( 2 \right)$
And for ray to pass through the second surface of the prism incident angle should be less than or equal to the critical angle.
${{R}_{2}}\le C$
From $\left( 2 \right)$
$A\le C$
So this is the condition for ray to emerge from the second face of the prism.

So the correct option is C.

Note:
In the condition for minimum deviation for the refraction in prism,
${{R}_{1}}={{R}_{2}}$
$A=\dfrac{R}{2}$
Also the incident angle in the first surface of the prism equals the emergent angle from the second surface of the prism in case of condition for minimum deviation.
Another equation for refraction in prism is
$i+e=A+\xi $
Where $i$ is incident angle on the first surface of prism,$e$ is emergent angle from the second surface of the prism $A$ is angle of prism and $\xi $is angle of minimum deviation.