Question

A ray of light travels from an optically denser medium to a rarer medium. The critical angle along the two media is ‘c’. What is the maximum possible deviation of the ray?

Answer 1

Hint: When a light ray goes from a denser to the rarer medium it bends away from the normal. So when the light ray strikes the denser to the rarer medium boundary at a particular angle it shows maximum deviation.

Complete step-by-step answer:
According to theory of refraction, the light coming from a denser to rarer medium bends away from the normal. So when the angle of incidence is ${{\text{ }\!\!\theta\!\!\text{ }}_{\text{i}}}$ in the denser medium and the angle of refraction is ${{\text{ }\!\!\theta\!\!\text{ }}_{\text{r}}}$in the rarer medium, the angle of refraction will always be greater than angle of incidence $\left( {{\text{ }\!\!\theta\!\!\text{ }}_{\text{r}}}\text{}{{\text{ }\!\!\theta\!\!\text{ }}_{\text{i}}} \right)$, since the light is travelling from a denser to rarer medium. The behavior is shown in the figure below.

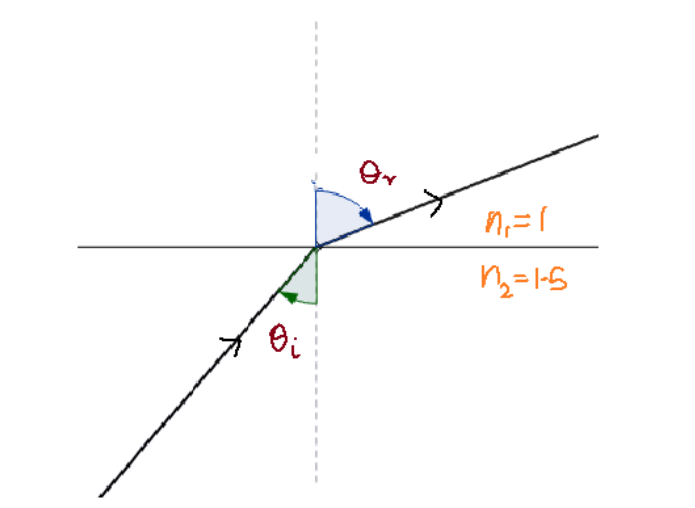
We know that according to snell’s law, ${{n}_{d}}\sin {{\theta }_{i}}={{n}_{r}}\sin {{\theta }_{r}}$
Where,
${{\text{n}}_{\text{d}}}$ is the refractive index of the denser medium.
${{\text{n}}_{\text{r}}}$ is the refractive index of the rarer medium.
So the angle of deviation or angle of refraction will be maximum when $\sin {{\theta }_{r}}$ is maximum. So it will be maximum at an angle of ${{90}^{\circ }}$. Which means that the refracted beam will grace the surface of the boundary as shown in the figure below. The angle of incidence for which this occurs is known as the critical angle for the two media. In our problem, it is given as ‘c’. So the maximum deviation at the critical angle will be ${{90}^{\circ }}$.

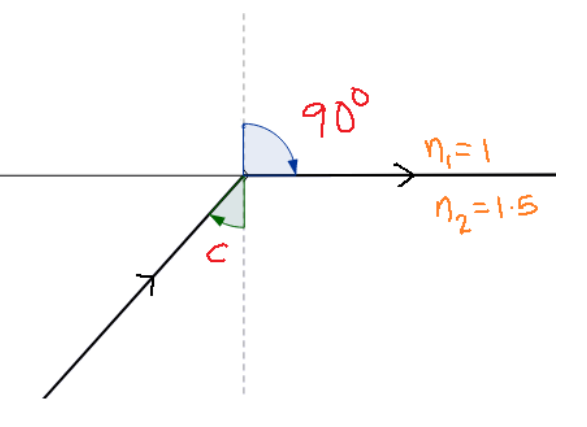
Note: So, applying these conditions in Snell’s law, we get,
${{n}_{d}}\sin \left( c \right)={{n}_{r}}\sin \left( {{90}^{\circ }} \right)$
$\dfrac{{{n}_{d}}}{{{n}_{r}}}=\dfrac{1}{\sin (c)}$
So, we can find the relative refractive index of a denser to rarer medium, by knowing only the critical angle of the denser medium.
Refraction is an important optical phenomenon that leads to many optical interactions we see in nature.
The critical angle is only achieved by a light going from a denser medium to a rare medium, and not the other way.