Question

A rectangle inscribed in a triangle has its base coinciding with the base b of the triangle. If the altitude of the triangle is h, and the altitude x of the rectangle is half the base of the rectangle, then:
A. \[x=\dfrac{1}{2}h\]
B. \[x=\dfrac{bh}{h+b}\]
C. \[x=\dfrac{bh}{2h+b}\]
D. \[x=\sqrt{\dfrac{hb}{2}}\]

Answer 1

Hint: As we can see that the rectangle DEFG is inscribed in a triangle ABC as per given question and AN represents an altitude from vertex A of triangle equal to \[h\] units (given) and the base of triangle of length b units. We can see that the altitude of rectangle is already given of \[x\] units. We use the concept of similarity of triangles to find the final answer.

Complete step-by-step answer:
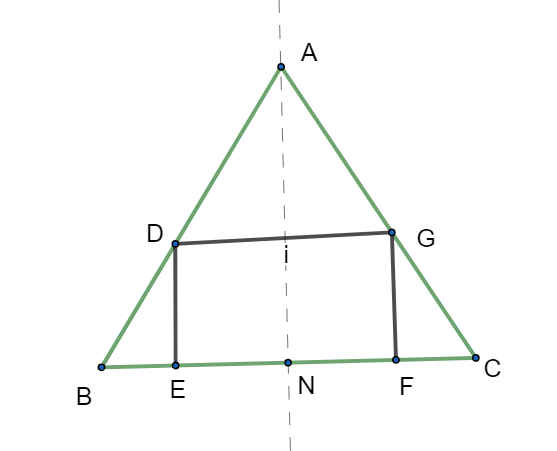
As we can see that the rectangle DEFG is inscribed in a triangle ABC as per given question and AN represents an altitude from vertex A of triangle equal to \[h\] units (given) and the base of triangle of length b units. We can see that the altitude of the rectangle is already given by \[x\] units.
In mathematics, we say that two objects are similar if they have the same shape, but not necessarily the same size. This means that we can obtain one figure from the other through a process of expansion or contraction, possibly followed by translation, rotation or reflection; these processes are known as transformations. If the objects also have the same size, they are congruent.
As altitude AN divides the triangle ABC into two unequal triangles ABN and ANC, we can apply similarity of triangles on both these triangles. Firstly taking triangle ABN where triangles BDE and ABN are similar triangle by angle-angle axioms (AA axiom of similarity of triangles),
Taking triangles ABN and BDE, let \[BN=k\] units and \[BE=p\] units,
Now using similarity of triangle’s,
\[\dfrac{AN}{BN}=\dfrac{DE}{BE}\]
\[\dfrac{h}{k}=\dfrac{x}{{{p}_{1}}}\]
\[{{p}_{1}}=\dfrac{kx}{h}\]
Secondly taking triangle ABN where triangles GFC and ANC are similar triangle by angle-angle axioms (AA axiom of similarity of triangles),
Taking triangles GFC and ANC, and using similarity of triangle’s we get,
\[\dfrac{AN}{NC}=\dfrac{GF}{FC}\]
\[\dfrac{h}{b-k}=\dfrac{x}{{{p}_{2}}}\]
\[{{p}_{2}}=\dfrac{(b-k)x}{h}\]
As we know BE+EF+FS is equals to BC (= b units), finding value of EF by rearranging,
\[EF=BC-BE-FC\]
\[EF=BC-({{p}_{1}}+{{p}_{2}})\]
\[EF=b-\left( \dfrac{kx}{h}+\dfrac{(b-k)x}{h} \right)\]
\[EF=b\left( 1-\dfrac{x}{h} \right)\]
Now as the altitude of rectangle x is given to be of half the size of its base, we get,
\[DE=\dfrac{EF}{2}\]
\[X=\dfrac{b}{2}\left( 1-\dfrac{x}{h} \right)\]
\[2hx=bh-bx\]
\[x(b+2h)=bh\]
\[x=\dfrac{bh}{b+2h}\]
Finally, we get value of x equal to \[x=\dfrac{bh}{b+2h}\],

So, the correct answer is “Option C”.

Note: The student must be familiar with the concept of similar triangles and congruence of triangles in addition to some of their properties. The common mistakes committed by students include wrong substitution in ratios and inability to understand which triangle or rectangle to take first to find proportions.