
A rectangle is to have an area of 16 square inches. How do you find its dimensions so that the distance from one corner to the midpoint of a nonadjacent side is a minimum?
Answer
461.7k+ views
Hint: To solve the above question, we should know about the rectangle. A rectangle is a 2D shape in geometry, having 4 sides and 4 corners. Its two sides meet at right angles. It has 4 angles, each measuring 90 degrees. The sides of a rectangle have the same lengths and are parallel. The area of the rectangle is
Complete step-by-step solution:
We have given that the area of the rectangle is
We can write is also as:
Now by using question we will draw a diagram of the line cutting through the rectangle and use the Pythagorean Theorem which is as:
Let
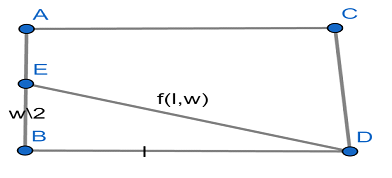
Now we will find the length of hypotenuse say
Now by using the area equation
Now substitute
Now solving the above equation we get
So by the above equation the value
Since we have to find the minimum value of
Now by using quotient rule
Now by more simplifying, we get
Now set the above equation equals to zero, we get
Now add
Therefore the derivative of
Now we have to find the extrema, first find the function values for the endpoints of the domain,
Since
Therefore,
Note: We can go wrong by creating the Pythagorean formula, here I created by using
Complete step-by-step solution:
We have given that the area of the rectangle is
We can write is also as:
Now by using question we will draw a diagram of the line cutting through the rectangle and use the Pythagorean Theorem which is as:
Let

Now we will find the length of hypotenuse say
Now by using the area equation
Now substitute
Now solving the above equation we get
So by the above equation the value
Since we have to find the minimum value of
Now by using quotient rule
Now by more simplifying, we get
Now set the above equation equals to zero, we get
Now add
Therefore the derivative of
Now we have to find the extrema, first find the function values for the endpoints of the domain,
Since
Therefore,
Note: We can go wrong by creating the Pythagorean formula, here I created by using
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




