
A rectangular glass slab ABCD of refractive index
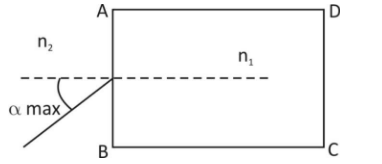
A.
B.
C.
D.

Answer
492k+ views
Hint:Concept of Total internal reflection is to be used. Then by shell’s law, the maximum value of
Formula used:
1. Snell’s law
2.
Where i is the angle of incidence
R is the angle of refraction
The ray travel from medium having refractive index
Complete step by step answer:
For the ray to emerge from the face CD, it has to undergo total interval reflection at face AD firstly as shown in the figure.
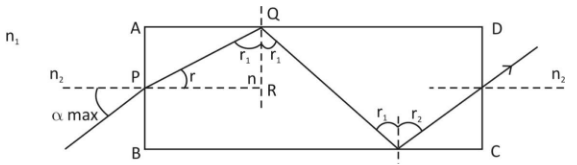
For total interval reflection to take place, angle of incidence,
i.e.
Now,
Now, let corresponding
We know that,
So,
Now, we know that by Snell’s law the ratio of
So, for the face AB, by applying Snell’s law, we have
(as here angle of incidence
Putting equation (2) in it, we get
Putting
We have
Hence, option (A) is the correct option.
Note:
This is because
Formula used:
1. Snell’s law
2.
Where i is the angle of incidence
R is the angle of refraction
The ray travel from medium having refractive index
Complete step by step answer:
For the ray to emerge from the face CD, it has to undergo total interval reflection at face AD firstly as shown in the figure.

For total interval reflection to take place, angle of incidence,
i.e.
Now,
Now, let corresponding
We know that,
So,
Now, we know that by Snell’s law the ratio of
So, for the face AB, by applying Snell’s law, we have
(as here angle of incidence
Putting equation (2) in it, we get
Putting
We have
Hence, option (A) is the correct option.
Note:
This is because
Latest Vedantu courses for you
Grade 10 | MAHARASHTRABOARD | SCHOOL | English
Vedantu 10 Maharashtra Pro Lite (2025-26)
School Full course for MAHARASHTRABOARD students
₹31,500 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




