Question

A rectangular park is 100 m by 50 m. It is surrounded by semi-circular flower beds all around. Find the cost of levelling the semi-circular flower beds at 60 paisa per square metre (Use $\pi = 3.14$).

Answer 1

Hint- Here, we will be proceeding by calculating the total area of semi-circular flower beds using the formula of area of a semi-circle which is given by \[\dfrac{{\pi {{\left( {\text{R}} \right)}^2}}}{2}\].

Complete step-by-step answer:
Given, Length of the rectangular park= 100 m
Breadth of the rectangular park= 50 m

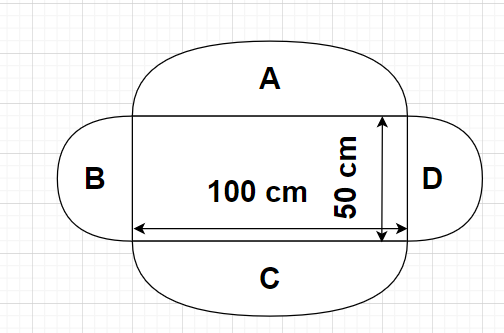
Since, 1 paisa = Rs $\dfrac{1}{{100}}$

Rate of levelling the semi-circular flower beds= 60 paisa per ${{\text{m}}^2}$ = Rs 0.6 per ${{\text{m}}^2}$

The cost of levelling the semi-circular flower beds which are there around the rectangular park is required. This cost of levelling depends upon the total area of the semi-circular flower beds.

Clearly, from the figure we can see that there are a total four semi-circular flower beds around the rectangular park out of which two of them (A and C) have equal diameters and the other two (B and D) also have equal diameters. If diameters are equal that means radius is also equal and hence areas will also be equal.

From the figure, Diameter of semi-circular flower bed A = Length of rectangular park = 100 m
As we know that, Radius of a circle$ = \dfrac{{{\text{Diameter of the circle}}}}{2}$

So, Radius of semi-circular flower bed A $ = \dfrac{{100}}{2} = 50$ m
Also we know that, Area of a semi-circle with a radius R \[ = \dfrac{{\pi {{\left( {\text{R}} \right)}^2}}}{2}\]

Area of semi-circular flower bed A $ = \dfrac{{\pi {{\left( {50} \right)}^2}}}{2} = \dfrac{{3.14 \times {{\left( {50} \right)}^2}}}{2} = 3925{\text{ }}{{\text{m}}^2}$

Since, semi-circular flower beds A and C will be having equal diameters and hence equal areas.
So, Area of semi-circular flower bed C = 3925 ${{\text{m}}^2}$
Again from the figure, Diameter of semi-circular flower bed B = Breadth of rectangular park = 50 m
As we know that, Radius of a circle$ = \dfrac{{{\text{Diameter of the circle}}}}{2}$
So, Radius of semi-circular flower bed B $ = \dfrac{{50}}{2} = 25$ m
Also we know that, Area of a semi-circle with a radius R \[ = \frac{{\pi {{\left( {\text{R}} \right)}^2}}}{2}\]

Area of semi-circular flower bed B $ = \dfrac{{\pi {{\left( {25} \right)}^2}}}{2} = \dfrac{{3.14 \times {{\left( {25} \right)}^2}}}{2} = 981.25{\text{ }}{{\text{m}}^2}$
Since, semi-circular flower beds B and D will be having equal diameters and hence equal areas.

So, Area of semi-circular flower bed D = 981.25 ${{\text{m}}^2}$

Total area of all the semi-circular flower beds is equal to the sum of all the areas of semi-circular beds A, B, C and D.
Total area of semi-circular flower beds = Area of semi-circular flower bed A + Area of semi-circular flower bed B + Area of semi-circular flower bed C + Area of semi-circular flower bed D
$ \Rightarrow $ Total area of semi-circular flower beds = 3925+981.25+3925+981.25 = 9812.5 ${{\text{m}}^2}$.

Since, Total cost of levelling the semi-circular flower beds = Rate of levelling the semi-circular flower beds$ \times $ Total area of semi-circular flower beds
$ \Rightarrow $ Total cost of levelling the semi-circular flower beds.

Therefore, the total cost of levelling the semi-circular flower beds at 60 paisa per square metre is Rs 5887.5

Note- In these types of problems, it is very important to make sure that if the unit of rate of levelling the semi-circular flower beds is Rs per ${{\text{m}}^2}$ (these units are obtained by converting the unit paisa per ${{\text{m}}^2}$ into Rs per ${{\text{m}}^2}$) then the unit of total area of the all the semi-circular beds should be in ${{\text{m}}^2}$.