Question

A regular pentagon and a regular decagon have the same perimeter then their areas are in the ratio
\[\left( \text{a} \right)\text{ }\sqrt{5}:1\]
\[\left( \text{b} \right)\text{ }\sqrt{5}:2\]
\[\left( \text{c} \right)\text{ 1:}\sqrt{5}\]
\[\left( \text{d} \right)\text{ 2:}\sqrt{5}\]

Answer 1

Hint: To solve the given question, we will first find out what regular pentagon is and what a regular decagon is. Then we will assume that their perimeter is ‘s’. Then we will find out their side lengths in terms of s. Then we will find the length of apothem in both the polygons. After this, we will find the areas of the triangles forming from joining the centre to two adjacent vertices in both the cases. In the case of the pentagon, we will multiply it by 5 and in the case of a decagon, we will multiply it by 10 to find the total area in both the cases.

Complete step by step solution:
Before we solve the given question, we must know that a pentagon is a polygon having five sides and a decagon is a polygon having ten sides. Let us assume that the side length of the pentagon is x and the side length of the decagon is y. It is given that both the polygons have the same perimeter. Let this perimeter be s. Now, there are five sides of the same length in a regular pentagon. Thus, we will get,
\[5x=s\]
\[\Rightarrow x=\dfrac{s}{5}......\left( i \right)\]
Similarly, there are 10 sides of the same length in a regular decagon. Thus, we will get,
\[10y=s\]
\[\Rightarrow y=\dfrac{s}{10}......\left( ii \right)\]
The rough sketch of the regular pentagon and regular decagon are shown below.

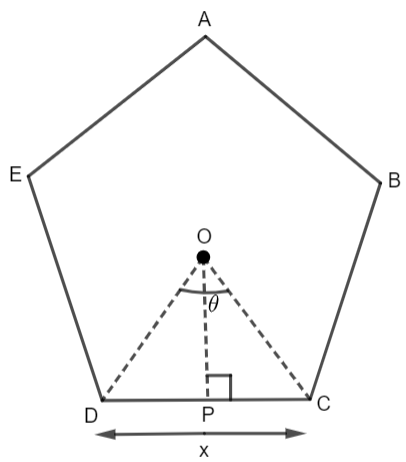
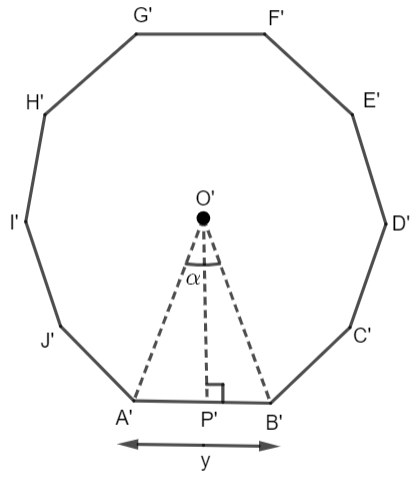
In the above pentagon OP is the apothem and in the above decagon O’P’ is the apothem. Now, \[\angle DOC=\theta \] and \[\angle {{A}^{'}}{{O}^{'}}{{B}^{'}}=\alpha .\] There are five equal sides in a regular pentagon and each side subtends an angle \[\theta \] on the centre. Thus,
\[5\theta ={{360}^{\circ }}\]
\[\Rightarrow \theta =\dfrac{{{360}^{\circ }}}{5}\]
\[\Rightarrow \theta ={{72}^{\circ }}.......\left( iii \right)\]
Now, there are 10 equal sides in a regular decagon and each side subtends an angle of \[\alpha \] on the centre. Thus,
\[10\alpha ={{360}^{\circ }}\]
\[\Rightarrow \alpha =\dfrac{{{360}^{\circ }}}{10}\]
\[\Rightarrow \alpha ={{36}^{\circ }}.......\left( iv \right)\]
Now, we will find the lengths of apothem in both cases. Now, we will consider the triangle POC. In triangle POC, we can say that,
\[\tan \left( \angle POC \right)=\dfrac{PC}{PO}\]
\[\Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{\left( \dfrac{x}{2} \right)}{OP}\]
\[\Rightarrow \tan \left( \dfrac{\theta }{2} \right)=\dfrac{x}{2\left( OP \right)}\]
Now, we will substitute the value of x and \[\theta \] from (i) and (iii) to the above equation. Thus, we will get,
\[\tan \left( \dfrac{\pi }{2} \right)=\dfrac{\dfrac{s}{5}}{2\left( OP \right)}\]
\[\Rightarrow \tan {{36}^{\circ }}=\dfrac{s}{10\left( OP \right)}\]
\[\Rightarrow OP=\dfrac{s}{10\left( \tan {{36}^{\circ }} \right)}......\left( v \right)\]
Now, we will calculate the area of triangle DOC. We know that the area of any triangle with base b and height is \[\dfrac{b.h}{2}.\] In our case, b = CD and h = OP. Thus,
\[\text{Area of }\Delta DOC=\dfrac{\left( CD \right)\left( OP \right)}{2}\]
\[\Rightarrow \text{Area of }\Delta DOC=\dfrac{\left( x \right)\left( OP \right)}{2}\]
Now, the area of the pentagon will be five times the area of triangle DOC. Thus,
\[\text{Area of pentagon}=\dfrac{5}{2}\left( x \right)\left( OP \right)......\left( vi \right)\]
Now, we will consider triangle O’P’B’. In triangle O’P’B’, we can say that,
\[\tan \left( \angle {{P}^{'}}{{O}^{'}}{{B}^{'}} \right)=\dfrac{{{P}^{'}}{{B}^{'}}}{{{P}^{'}}{{O}^{'}}}\]
\[\Rightarrow \tan \left( \dfrac{\angle {{A}^{'}}{{O}^{'}}{{B}^{'}}}{2} \right)=\dfrac{\left( \dfrac{y}{2} \right)}{{{P}^{'}}{{O}^{'}}}\]
\[\Rightarrow \tan \left( \dfrac{\alpha }{2} \right)=\dfrac{y}{2\left( {{P}^{'}}{{O}^{'}} \right)}\]
Now, we will substitute the value of y and \[\alpha \] from (ii) and (iv) to the above equation. Thus, we will get,
\[\tan \left( \dfrac{{{36}^{\circ }}}{2} \right)=\dfrac{\dfrac{s}{10}}{2\left( {{P}^{'}}{{O}^{'}} \right)}\]
\[\Rightarrow \tan {{18}^{\circ }}=\dfrac{s}{20\left( {{P}^{'}}{{O}^{'}} \right)}\]
\[\Rightarrow {{P}^{'}}{{O}^{'}}=\dfrac{s}{20\left( \tan {{18}^{\circ }} \right)}.......\left( vii \right)\]
Now, we will calculate the area of triangle A’O’B’. Thus, we have,
\[\Rightarrow \text{Area of }\Delta {{A}^{'}}{{O}^{'}}{{B}^{'}}=\dfrac{y\left( {{O}^{'}}{{P}^{'}} \right)}{2}\]
Now, the area of decagon will be 10 times the area of triangle A’O’B’. Thus,
\[\text{Area of decagon}=10\times \left( \text{Area of }\Delta {{\text{A}}^{'}}{{O}^{'}}{{B}^{'}} \right)\]
\[\Rightarrow \text{Area of decagon}=10\times \left( \dfrac{1}{2}\times y\times {{O}^{'}}{{P}^{'}} \right)\]
\[\Rightarrow \text{Area of decagon}=5\left( y \right)\left( {{O}^{'}}{{P}^{'}} \right)......\left( viii \right)\]
Now, we have to find their ratios. So, we will divide (vi) by (viii). Thus, we will get,
\[\dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{\dfrac{5}{2}\left( x \right)\left( OP \right)}{5\left( y \right)\left( {{O}^{'}}{{P}^{'}} \right)}\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{\left( x \right)\left( OP \right)}{2\left( y \right)\left( {{O}^{'}}{{P}^{'}} \right)}\]
Now, we will put the values of x, y, OP and O’P’ in the above equation.
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{\left( \dfrac{s}{5} \right)\left( \dfrac{s}{10\tan {{36}^{\circ }}} \right)}{2\left( \dfrac{s}{10} \right)\left( \dfrac{s}{20\tan {{18}^{\circ }}} \right)}\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{10\times 20\tan {{18}^{\circ }}}{2\times 5\times 10\tan {{36}^{\circ }}}\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{2\tan {{18}^{\circ }}}{\tan {{36}^{\circ }}}......\left( ix \right)\]
Now, we know that, \[\tan 2A=\dfrac{2\tan A}{1-{{\tan }^{2}}A}.\] Here, we will put \[A={{18}^{\circ }}.\] Thus, we will get,
\[\tan {{36}^{\circ }}=\dfrac{2\tan {{18}^{\circ }}}{1-{{\tan }^{2}}{{18}^{\circ }}}\]
\[\Rightarrow \dfrac{2\tan {{18}^{\circ }}}{\tan {{36}^{\circ }}}=1-{{\tan }^{2}}{{18}^{\circ }}........\left( x \right)\]
From (ix) and (x), we will get,
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=1-{{\tan }^{2}}{{18}^{\circ }}......\left( xi \right)\]
Now, we will find the value \[{{\tan }^{2}}{{18}^{\circ }}.\] We know that,
\[\sin {{18}^{\circ }}=\dfrac{\sqrt{5}-1}{4}\]
Squaring both the sides, we get,
\[\Rightarrow {{\sin }^{2}}{{18}^{\circ }}={{\left( \dfrac{\sqrt{5}-1}{4} \right)}^{2}}\]
\[\Rightarrow {{\sin }^{2}}{{18}^{\circ }}=\dfrac{{{\left( \sqrt{5} \right)}^{2}}-2\left( \sqrt{5} \right)\left( 1 \right)+{{\left( 1 \right)}^{2}}}{{{\left( 4 \right)}^{2}}}\]
\[\Rightarrow {{\sin }^{2}}{{18}^{\circ }}=\dfrac{6-2\left( \sqrt{5} \right)}{16}\]
\[\Rightarrow {{\sin }^{2}}{{18}^{\circ }}=\dfrac{3-\left( \sqrt{5} \right)}{8}\]
Now, we know that,
\[{{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1\]
\[\Rightarrow {{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \]
\[\Rightarrow {{\cos }^{2}}{{18}^{\circ }}=1-{{\sin }^{2}}{{18}^{\circ }}\]
\[\Rightarrow {{\cos }^{2}}{{18}^{\circ }}=1-\dfrac{3-\sqrt{5}}{8}\]
\[\Rightarrow {{\cos }^{2}}{{18}^{\circ }}=\dfrac{5+\sqrt{5}}{8}\]
Now, we know that, \[\dfrac{\sin \theta }{\cos \theta }=\tan \theta .\] On squaring both the sides, we will get,
\[\dfrac{{{\sin }^{2}}\theta }{{{\cos }^{2}}\theta }={{\tan }^{2}}\theta \]
On putting, \[\theta ={{18}^{\circ }},\] we will get,
\[{{\tan }^{2}}{{18}^{\circ }}=\dfrac{{{\sin }^{2}}{{18}^{\circ }}}{{{\cos }^{2}}{{18}^{\circ }}}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{\left( \dfrac{3-\sqrt{5}}{8} \right)}{\left( \dfrac{5+\sqrt{5}}{8} \right)}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{3-\sqrt{5}}{5+\sqrt{5}}\]
On rationalising the RHS, we will get,
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{3-\sqrt{5}}{5+\sqrt{5}}\times \dfrac{\left( 5-\sqrt{5} \right)}{\left( 5-\sqrt{5} \right)}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{\left( 3-\sqrt{5} \right)\left( 5-\sqrt{5} \right)}{\left( 5+\sqrt{5} \right)\left( 5-\sqrt{5} \right)}\]
Using the identity \[\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}\] on the denominator, we get,
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{\left( 3-\sqrt{5} \right)\left( 5-\sqrt{5} \right)}{{{\left( 5 \right)}^{2}}-{{\left( \sqrt{5} \right)}^{2}}}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{15-3\sqrt{5}-5\sqrt{5}+5}{25-5}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{20-8\sqrt{5}}{20}\]
\[\Rightarrow {{\tan }^{2}}{{18}^{\circ }}=\dfrac{5-2\sqrt{5}}{5}\]
Now, we will put the value of \[{{\tan }^{2}}{{18}^{\circ }}\] in (xi). Thus, we will get,
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=1-\left( \dfrac{5-2\sqrt{5}}{5} \right)\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{5-5+2\sqrt{5}}{5}\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{2\sqrt{5}}{5}\]
\[\Rightarrow \dfrac{\text{Area of pentagon}}{\text{Area of decagon}}=\dfrac{2}{\sqrt{5}}\]
Hence, option (d) is the right answer.

Note: The area of pentagon and decagon can also be found out in an alternate way. The area of a regular polygon with side length ‘t’ and number of sides ‘n’ is given by
\[\text{Area of polygon}=\dfrac{{{t}^{2}}n}{4\tan \left( \dfrac{{{180}^{\circ }}}{n} \right)}\]
When we will put the respective values of t and n in the above formula, we will get the area of the regular decagon and regular pentagon.