
Answer
464.7k+ views
Hint: A right circular cylinder is a cylinder whose base is a circle and whose elements are perpendicular to its base. Here, the height of the cylinder and diameter of the sphere are the same.
Formulas used: Surface area of a sphere is $4\pi {r^2}$ where ‘r’ is the radius of the sphere and \['\pi '\] is equal to 22/7 or 3.14.
Curved surface area of the cylinder is $2\pi rh$ where ‘r’ is the radius of the base of the cylinder and ‘h’ is the height of the cylinder.
Complete step-by-step answer:
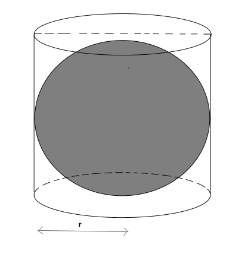
Given that the right circular cylinder encloses a sphere of radius r.
From the figure, we get that the diameter of the sphere and height of the cylinder are the same and also the diameter of the sphere and the diameter of the base of the cylinder are the same.
Given that the radius of the sphere is ‘r’ which means the diameter of the sphere is ‘2r’.
Therefore, the height of the cylinder is ‘2r’ and radius of the base of the cylinder is ‘r’. $ \to statement1$
(i) Surface area of the sphere
Surface area of the sphere is $4\pi {r^2}$
As we know that the radius of the sphere given is ‘r’, the surface area of the sphere is the same which is $4\pi {r^2}$ .
(ii)Curved surface area of the cylinder
Curved surface area of the cylinder is $2\pi rh$
h=2r and r=r from the statement 1.
Finally curved surface area of the cylinder
$
= 2 \times \pi \times r \times 2r \\
= 2 \times 2 \times \pi \times r \times r \\
= 4\pi {r^2} \\
$
(iii) Ratio of surface areas obtained in (i) and (ii)
Ratio of surface area of the sphere and curved surface area of the cylinder =
Surface area of the sphere/Curved surface area of the cylinder
Surface area of the sphere obtained is $4\pi {r^2}$ .
Curved surface area of the cylinder obtained is $4\pi {r^2}$ .
Therefore, the ratio is
$
= \dfrac{{4\pi {r^2}}}{{4\pi {r^2}}} \\
= \dfrac{1}{1} \\
= 1:1 \\
$
Therefore, the ratio of the surface area of the sphere and curved surface area of the cylinder is 1:1.
Note: A Circle is a two-dimensional figure whereas a Sphere is a three-dimensional object. So do not confuse a sphere with a circle.A right circular cylinder is a cylinder that has a closed circular surface having two parallel bases on both the ends and are perpendicular to its base. It is also known as a right cylinder.
Formulas used: Surface area of a sphere is $4\pi {r^2}$ where ‘r’ is the radius of the sphere and \['\pi '\] is equal to 22/7 or 3.14.
Curved surface area of the cylinder is $2\pi rh$ where ‘r’ is the radius of the base of the cylinder and ‘h’ is the height of the cylinder.
Complete step-by-step answer:

Given that the right circular cylinder encloses a sphere of radius r.
From the figure, we get that the diameter of the sphere and height of the cylinder are the same and also the diameter of the sphere and the diameter of the base of the cylinder are the same.
Given that the radius of the sphere is ‘r’ which means the diameter of the sphere is ‘2r’.
Therefore, the height of the cylinder is ‘2r’ and radius of the base of the cylinder is ‘r’. $ \to statement1$
(i) Surface area of the sphere
Surface area of the sphere is $4\pi {r^2}$
As we know that the radius of the sphere given is ‘r’, the surface area of the sphere is the same which is $4\pi {r^2}$ .
(ii)Curved surface area of the cylinder
Curved surface area of the cylinder is $2\pi rh$
h=2r and r=r from the statement 1.
Finally curved surface area of the cylinder
$
= 2 \times \pi \times r \times 2r \\
= 2 \times 2 \times \pi \times r \times r \\
= 4\pi {r^2} \\
$
(iii) Ratio of surface areas obtained in (i) and (ii)
Ratio of surface area of the sphere and curved surface area of the cylinder =
Surface area of the sphere/Curved surface area of the cylinder
Surface area of the sphere obtained is $4\pi {r^2}$ .
Curved surface area of the cylinder obtained is $4\pi {r^2}$ .
Therefore, the ratio is
$
= \dfrac{{4\pi {r^2}}}{{4\pi {r^2}}} \\
= \dfrac{1}{1} \\
= 1:1 \\
$
Therefore, the ratio of the surface area of the sphere and curved surface area of the cylinder is 1:1.
Note: A Circle is a two-dimensional figure whereas a Sphere is a three-dimensional object. So do not confuse a sphere with a circle.A right circular cylinder is a cylinder that has a closed circular surface having two parallel bases on both the ends and are perpendicular to its base. It is also known as a right cylinder.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

If the coordinates of the points A B and C be 443 23 class 10 maths JEE_Main

If the mean of the set of numbers x1x2xn is bar x then class 10 maths JEE_Main

What is the meaning of celestial class 10 social science CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE




