Question

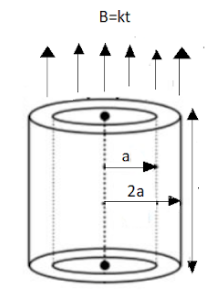
A ring of circular cross section is made up of material of resistivity $ \rho $ . The inner and outer radii of ring are $ a $ and $ 2a $ and its thickness is $ h $ , The ring is placed in a varying magnetic field $ B = kt $ (where $ k $ is a constant )which is parallel to the axis of the ring as shown in the figure . The induced current in the ring is :
 $ \left( A \right)\dfrac{{3kh{a^2}}}{{4\rho }} \\
  \left( B \right)\dfrac{{3kh{a^2}}}{{2\rho }} \\
  \left( C \right)\dfrac{{5kh{a^2}}}{{4\rho }} \\
  \left( D \right)\dfrac{{5kh{a^2}}}{{2\rho }} \\ $

Answer 1

Hint : In order to solve this question, we are going to first find the flux related to the ring of radius lying between the two radii, then from flux, the emf can be found very easily. Then, by finding the resistance from resistivity and the area and length, the total induced current can be calculated.
The flux related to a ring is given by
 $ \phi = BdA $
Emf is given by
 $ emf = \dfrac{{d\phi }}{{dt}} $

Complete Step By Step Answer:
Let us consider a hypothetical ring of radius $ r $ that exists in between the rings of radii $ a $ and $ 2a $ ,
The flux related to this ring is given by
 $ \phi = BdA $
Putting the values of the magnetic field as given in the question and the area, we get,
 $ \phi = kt \times \pi hdr $
Now as we know that the emf is defined as the rate of change of flux per unit time, i.e.,
Mathematically,
 $ emf = \dfrac{{d\phi }}{{dt}} = \dfrac{d}{{dt}}\left( {\pi kt hdr} \right) $
On solving this equation, further, we get,
 $ emf = \pi khdr $
Now, in order to find the current, we need two quantities emf and resistance, thus, the current is
calculated as
 $ i = \dfrac{{emf}}{R} $
Where, $ R = \dfrac{{\rho dr}}{{\pi rdr}} = \dfrac{\rho }{{\pi r}} $
Thus,
 $ i = \dfrac{{\pi khdr}}{{\dfrac{\rho }{{\pi r}}}} = \dfrac{{4{\pi ^2}kh\int_a^b {rdr} }}{\rho } $
On solving the integral, we get
 $ i = \dfrac{{{\pi ^2}kh\left( {4{a^2} - {a^2}} \right)}}{{2\rho }} \\
   \Rightarrow i = \dfrac{{3{\pi ^2}kh{a^2}}}{{2\rho }} \\ $

Note :
It is to be noted that the flux that is found for a ring of the radius lying between the two radii, is the same for the total flux too and the resistance is found for the whole ring at once. The emf that is calculated gives the induced emf from the whole surface area from which the magnetic field lines are passing.