Question

A road, 14m wide, surrounds a circular park whose circumference is 704m. Find the surface area of the road. Also, find the cost of paving the road at Rs. 100 per meter square.

Answer 1

Hint: First, before proceeding for this, we must draw two concentric circles with inner circle representing the circular park whose circumference is given and outer circle represent the circle made by extending the road by 14m from the inner circle. Then, we are given the question that the inner circle has the circumference of 704m and we also know that the circumference C of the circle with radius r is given by $C=2\pi r$. Then, we also know from the study of circles that area A of the circle with radius r is given by $A=\pi {{r}^{2}}$, using both circles, we get the desired results.

Complete step-by-step answer:
In this question, we are supposed to find the surface area of the road and cost of paving it at a cost of Rs. 100 per metre square when the road, 14m wide, surrounds a circular park whose circumference is 704m.
So, before proceeding for this, we must draw two concentric circles with inner circle representing the circular park whose circumference is given and outer circle represent the circle made by extending the road by 14m from inner circle as:

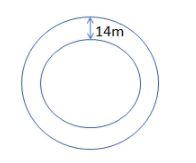
Then, we are given in the question that inner circle has the circumference of 704m and we also know that the circumference C of the circle with radius r is given by:
$C=2\pi r$
Then, by substituting the value of C from the question which is 704, we get the value of inner radius r as:
$\begin{align}
  & 704=2\times \dfrac{22}{7}\times r \\
 & \Rightarrow r=\dfrac{704\times 7}{2\times 22} \\
 & \Rightarrow r=112 \\
\end{align}$
So, we get the radius of the inner circle as 112m.
Then we also know from the study of circles that area A of the circle with radius r is given by:
$A=\pi {{r}^{2}}$
So, by substituting the value of r calculated above as 112m in the area formula to get the area ${{A}_{1}}$ of inner circle as:
$\begin{align}
  & {{A}_{1}}=\pi {{\left( 112 \right)}^{2}} \\
 & \Rightarrow {{A}_{1}}=\dfrac{22}{7}\times 112\times 112 \\
 & \Rightarrow {{A}_{1}}=39424 \\
\end{align}$
So, we get the area of the inner circle as 39424 meter square.
Then, by using the same formula for outer circle but its radius R becomes the summation of the inner radius and the road width as:
R=r+14
$\begin{align}
  & \Rightarrow R=112+14 \\
 & \Rightarrow R=126 \\
\end{align}$
Now, by substituting the value of R calculated above as 126m in the area formula to get the area ${{A}_{2}}$ of outer circle as:
$\begin{align}
  & {{A}_{2}}=\pi {{\left( 126 \right)}^{2}} \\
 & \Rightarrow {{A}_{2}}=\dfrac{22}{7}\times 126\times 126 \\
 & \Rightarrow {{A}_{2}}=49896 \\
\end{align}$
So, we get the area of the outer circle as 49896 metre square.
Now, we need to calculate the area between the two circles which is given by the difference of ${{A}_{2}}$and ${{A}_{1}}$as:
$\begin{align}
  & {{A}_{2}}-{{A}_{1}}=49896-39424 \\
 & \Rightarrow {{A}_{2}}-{{A}_{1}}=10472 \\
\end{align}$
So, we get the surface area of the road as 10472 meter square.
Now, we are supposed to find the cost of paving the road at Rs. 100 per square meter is given by:
$\begin{align}
  & 10472\times 100 \\
 & \Rightarrow 1047200 \\
\end{align}$
So, we get the cost of paving as Rs. 1047200.
Hence, the area of the road is $10472{{m}^{2}}$ and the cost of paving it as Rs. 1047200.

So, the correct answer is “Option A”.

Note: Now, to solve these types of questions we need to know some of the basic formulas of the circle beforehand to solve the question easily and appropriately. So, the required formulas are as:
Area of the circle with radius r is given by $\pi {{r}^{2}}$.
Circumference of the circle with radius r is given by $2\pi r$.
Using any value of $\pi $as $\dfrac{22}{7}$ or 3.14 both will give the nearly same result.