Question

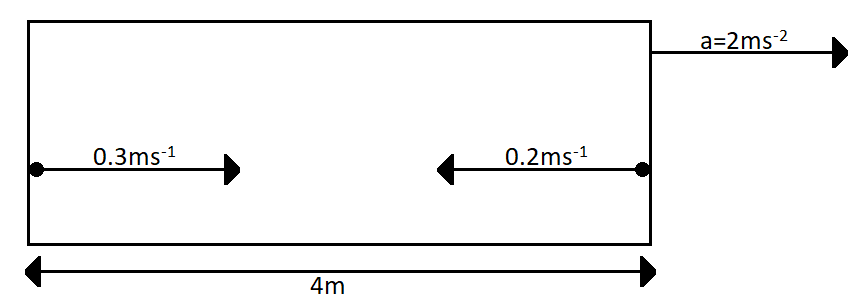
A rocket is moving in a gravity free space with a constant acceleration of $ 2m{s^{ - 2}} $ along +x direction (see figure). The length of a chamber inside the rocket is $ 4m $. A ball is thrown from the left end of the chamber in +x direction with a speed of $ 0.3m{s^{ - 1}} $ relative to the rocket. At the same time, another ball is thrown in –x direction with a speed of $ 0.2m{s^{ - 1}} $ from its right end relative to the rocket. The time in seconds when the two balls hit each other is

Answer 1

Hint
For the right ball the acceleration is in the negative direction. So if we consider, the right ball travels a distance $ S $, then using the initial velocity, we can find the value of $ S $ in terms of the time. Similarly we can do the same for the case of the left ball where the distance travelled by the left ball will be $ 4 - S $. By solving the two equations we can get the time.

Formula Used: In this solution we will be using the following formula,
 $\Rightarrow S = ut + \dfrac{1}{2}a{t^2} $
where $ S $ is the distance travelled, $ u $ is the initial velocity, $ a $ is the acceleration, $ t $ is the time taken.

Complete step by step answer
Let us redraw the diagram and name the two balls as A and b and also mark the point of their collision. So we have,

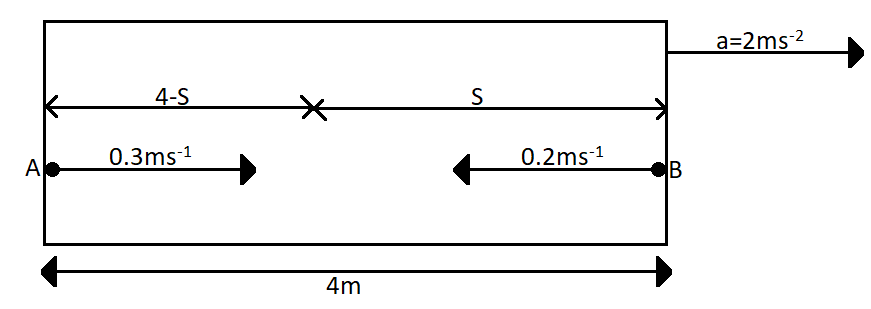
Now let us first consider the ball B. The ball is released with an initial velocity of $ 0.2m{s^{ - 1}} $. The ball is travelling in a direction which is opposite to the direction of the acceleration of the rocket. So the acceleration of the ball will be $ - 2m{s^{ - 2}} $. Let the ball travel a distance of $ S $, after which the collision takes place. So we can find the value of $ S $ from the equation of motion given by,
 $\Rightarrow S = ut + \dfrac{1}{2}a{t^2} $
Here $ t $ is the time at which the collision takes place. So substituting the values of the initial velocity and the acceleration we get,
 $\Rightarrow S = 0.2t + \dfrac{1}{2}\left( { - 2} \right){t^2} $
On simplifying we get,
 $\Rightarrow S = 0.2t - {t^2} $ ……(1)
Now let us consider the ball marked as A. The initial velocity of this ball is $ 0.3m{s^{ - 1}} $. And its direction of motion is the same as that of the rocket. So the acceleration of the ball will be, $ 2m{s^{ - 2}} $. Now since the whole length of the rocket is $ 4m $ and the ball B travels a distance $ S $ for collision, so the distance travelled by the ball A is $ 4 - S $. So again applying the equation of motion,
 $\Rightarrow 4 - S = 0.3t + \dfrac{1}{2}\left( 2 \right){t^2} $
Hence we get,
 $\Rightarrow S = 4 - 0.3t - {t^2} $ ……(2)
Now we can equate equations 1 and 2 and get,
 $\Rightarrow 0.2t - {t^2} = 4 - 0.3t - {t^2} $
On cancelling the $ {t^2} $ from both the sides and taking $ 0.3t $ from the RHS to the LHS we get,
 $\Rightarrow 0.2t + 0.3t = 4 $
Therefore, we have
 $\Rightarrow 0.5t = 4 $
By dividing both sided by $ 0.5 $ we get,
 $\Rightarrow t = \dfrac{4}{{0.5}} = 8s $
Therefore, the time in seconds when the two balls hit each other is $ 8s $.

Note
In this question we have considered the speed of the two balls relative to the speed of the rocket. So the absolute speeds of the balls are different than the given speed and for any observer watching from outside the rocket.