Question

A semi-circular ring of radius 0.5m is uniformly charged with the total charge of $1.4 \times 10^{-9}C$. The electric field intensity at the centre of the ring:
$\text{A.} \ 320Vm^{-1}$
$\text{B.} \ 0Vm^{-1}$
$\text{C.} \ 64Vm^{-1}$
$\text{D.} \ 32Vm^{-1}$

Answer 1

Hint: Here, it is important to note that the charge is distributed over an object. Hence we cannot directly apply Coulomb's law which is valid for point charge. Hence we need to get the electric field due to any general element and then integrate over the ring to get a net electric field at the centre.

Formula used:
$dE = \dfrac{Kdq}{r^2}$

Complete answer:

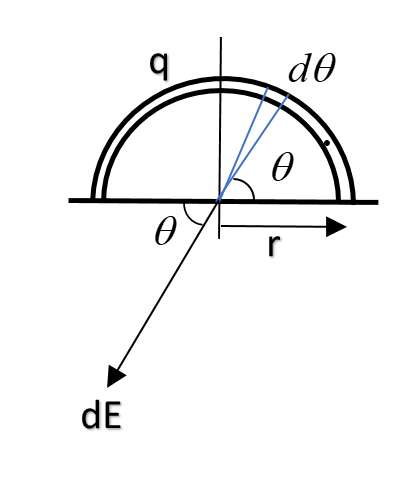
Let us consider an elementary part of the ring at an angle $\theta$ having angular length of $d\theta$. The small charge inside the elementary part will be calculated as follows:
Total circumference = $\pi r$
Total charge distributed = q
Hence the linear charge density = $\dfrac{q}{\pi r}$
Thus the total charge in the element of length $rd\theta$, will be:
$dq = \dfrac{q}{\pi r}rd\theta = \dfrac{qd\theta}{\pi}$
Now, using $dE = \dfrac{Kdq}{r^2}$
The field along –y axis is sin component of dE,
$dE_{y} = dE cos\theta = \dfrac{Kq}{\pi r^2}\times sin\theta d\theta$
Then, $E_{net} = \int dE = \int \dfrac{Kq}{\pi r^2} \times sin\theta d\theta$
[ where $E_{net}$= net field in –y direction]
Or, ${{E}_{net}}=\dfrac{Kq}{\pi {{r}^{2}}}\times \int\limits_{0}^{\pi }{sin\theta {d}}\theta$ [ as K. q and r are constants ]
As the material is present for $\theta = 0 \ to \ \theta = \pi$, hence are the limits.
And $E_{net} = \dfrac{Kq}{\pi r^2} \times (1-(-1)) = \dfrac{2Kq}{\pi r^2}$
Hence we get the net field in my direction.
On putting the values $q=1.4 \times 10^{-9}C$, r=0.5m, we get;
$E_{net} = \dfrac{2\times 9\times 10^9 \times 1.4 \times 10^{-9}}{3.14 \times 0.5^2} = 32 Vm^{-1}$

So, the correct answer is “Option D”.

Note:
Students here should note that we can write $E_{y} = E_{net}$ as due to symmetry, only y component of the field will contribute for the total field and x component will come out to be zero. This can also be easily proven by taking $dE_x = dE_{net} = \dfrac{Kq}{r^2}\times cos\theta$. Also students should understand how to take the limits. If the material were present only in the first quadrant, we might have taken the limits from 0 to $\dfrac{\pi}{2}$ instead of $\pi$.