Question

What is a series LCR resonant circuit? State conditions for series resonance. Obtain an expression for resonant frequency.

Answer 1

Hint: A series LCR resonant circuit consists of an inductor, a capacitor and a resistance. The resonance will occur in this circuit when the reactance of the circuit will be zero. By equating the reactance of capacitor and inductor, we can obtain the expression for resonant frequency.

Complete answer:
A LCR circuit consists of an inductor of inductance L, a capacitor of capacitance C and a resistor of resistance R and an AC voltage source. When they are connected in series combination, we obtain series LCR resonant circuit as shown in the diagram.

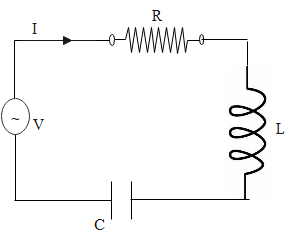
The resonance is obtained in these circuits when the reactance of the capacitor cancels the reactance of the inductor. The expressions for the reactance of a capacitor and an inductor are given as follows:
\[
  {X_C} = \dfrac{1}{{\omega C}} \\
  {X_L} = \omega L \\
\]
Here $\omega $ represents the frequency of the AC signal used in the signal.
When resonance occurs, the above expressions become equal to each other. By equating them we can get the condition for resonance in the series LCR circuit.
$
  {X_L} = {X_C} \\
  \omega L = \dfrac{1}{{\omega C}} \\
  {\omega ^2} = \dfrac{1}{{LC}} \\
   \Rightarrow \omega = \dfrac{1}{{\sqrt {LC} }} \\
$
This is the expression for resonant frequency for a series LCR circuit at which the resonance occurs. It is inversely related to the values of inductance and capacitance of the circuit.

Note:
1. During resonance, the current through the circuit becomes maximum because the reactance cancels each other as a result there is a fall in resistance of the circuit.
2. The resistor is unaffected by the variations in the AC signal as a result, it plays no role in resonance and remains constant. When resonance occurs in a series LCR circuit, the resistance of the circuit becomes equal to the resistance due to the resistance. By removing the resistance, we can get almost zero impedance at resonance.