
A shuttlecock used for playing badminton has the shape of a frustum of a cone mounted on a hemisphere. The external diameter of the frustum are 5 cm and 2 cm. The height of the entire shuttlecock is 7 cm. Find its external surface area.
Answer
522.3k+ views
Hint: First of all, draw the diagram of shuttlecock to visualize the question. Now find the slant height of the cock by using \[l=\sqrt{{{\left( {{r}_{2}}-{{r}_{1}} \right)}^{2}}+{{h}^{2}}}\]. Now, find the external surface area of the shuttlecock by adding the curved surface area of the frustum and hemispherical parts that are \[\pi \left( {{r}_{1}}+{{r}_{2}} \right)l\] and \[2\pi r_{1}^{2}\] respectively where \[{{r}_{1}}<{{r}_{2}}\].
Complete step by step answer:
We are given that a shuttlecock has the shape of the frustum of a cone mounted on the hemisphere. The external diameter of the frustum are 5cm and 2 cm and the height of the entire cock is 7 cm. We have to find the external surface area of the shuttlecock. Let us first see the figure of the shuttlecock.
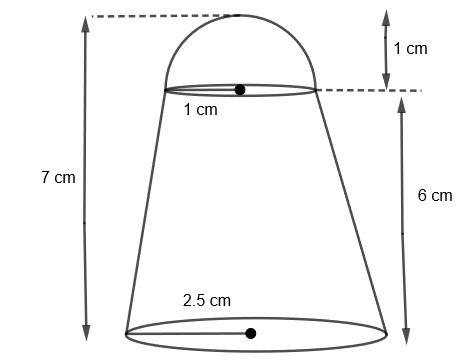
For the frustum of the shuttlecock, we are given that, radius \[\left( {{r}_{1}} \right)=\dfrac{5}{2}=2.5cm\] and radius \[\left( {{r}_{2}} \right)=\dfrac{2}{2}=1cm\]. Also, the height of the frustum would be h = (7 – 1) = 6 cm. We know that the slant height of the frustum is given by:
\[l=\sqrt{{{h}^{2}}+{{\left( {{r}_{2}}-{{r}_{1}} \right)}^{2}}}\]
By substituting the values of \[{{r}_{1}}\], \[{{r}_{2}}\] and h, we get the slant of the frustum as,
\[l=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 2.5-1 \right)}^{2}}}\]
\[l=\sqrt{36+2.25}\]
\[l=\sqrt{38.25}\]
\[l=6.18cm\]
We know that the external surface area of the shuttlecock = (curved surface area of the frustum) + (curved surface area of the hemisphere) …..(i)
We know that, the curved surface area of the frustum,
\[F=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l\]
By substituting the values of \[{{r}_{1}}\], \[{{r}_{2}}\] and l, we get,
\[F=\pi \left( 2.5+1 \right).6.18\]
\[=21.63\pi \text{ }c{{m}^{2}}\]
Now, we also know that the curved surface area of the hemisphere,
\[H=2\pi {{\left( {{r}_{2}} \right)}^{2}}\]
By substituting the value of \[{{r}_{2}}\], we get,
\[H=2\pi {{\left( 1 \right)}^{2}}=2\pi \text{ }c{{m}^{2}}\]
Now, by substituting the respective values in the RHS of the equation (i), we get the external surface area of the shuttlecock,
\[S=21.63\pi \text{ }c{{m}^{2}}+2\pi \text{ }c{{m}^{2}}\]
\[\Rightarrow \left( 21.63+2 \right)\pi \text{ }c{{m}^{2}}\]
By substituting the values of \[\pi =\dfrac{22}{7}\], we get,
\[S=23.63\times \dfrac{22}{7}c{{m}^{2}}\]
\[S=74.26\text{ }c{{m}^{2}}\]
Hence, we get the total external surface area of the shuttlecock as \[74.26\text{ }c{{m}^{2}}\].
Note: Students are always advised to draw the diagram first in these types of questions. Also, students should properly do the calculations and take care while putting the decimal in numbers. In this question, some students make this mistake of calculating the total surface area instead of curved surface area, but as we can see that, we only need a curved surface area here to calculate the external area. So this mistake must be taken care of.
Complete step by step answer:
We are given that a shuttlecock has the shape of the frustum of a cone mounted on the hemisphere. The external diameter of the frustum are 5cm and 2 cm and the height of the entire cock is 7 cm. We have to find the external surface area of the shuttlecock. Let us first see the figure of the shuttlecock.

For the frustum of the shuttlecock, we are given that, radius \[\left( {{r}_{1}} \right)=\dfrac{5}{2}=2.5cm\] and radius \[\left( {{r}_{2}} \right)=\dfrac{2}{2}=1cm\]. Also, the height of the frustum would be h = (7 – 1) = 6 cm. We know that the slant height of the frustum is given by:
\[l=\sqrt{{{h}^{2}}+{{\left( {{r}_{2}}-{{r}_{1}} \right)}^{2}}}\]
By substituting the values of \[{{r}_{1}}\], \[{{r}_{2}}\] and h, we get the slant of the frustum as,
\[l=\sqrt{{{\left( 6 \right)}^{2}}+{{\left( 2.5-1 \right)}^{2}}}\]
\[l=\sqrt{36+2.25}\]
\[l=\sqrt{38.25}\]
\[l=6.18cm\]
We know that the external surface area of the shuttlecock = (curved surface area of the frustum) + (curved surface area of the hemisphere) …..(i)
We know that, the curved surface area of the frustum,
\[F=\pi \left( {{r}_{1}}+{{r}_{2}} \right)l\]
By substituting the values of \[{{r}_{1}}\], \[{{r}_{2}}\] and l, we get,
\[F=\pi \left( 2.5+1 \right).6.18\]
\[=21.63\pi \text{ }c{{m}^{2}}\]
Now, we also know that the curved surface area of the hemisphere,
\[H=2\pi {{\left( {{r}_{2}} \right)}^{2}}\]
By substituting the value of \[{{r}_{2}}\], we get,
\[H=2\pi {{\left( 1 \right)}^{2}}=2\pi \text{ }c{{m}^{2}}\]
Now, by substituting the respective values in the RHS of the equation (i), we get the external surface area of the shuttlecock,
\[S=21.63\pi \text{ }c{{m}^{2}}+2\pi \text{ }c{{m}^{2}}\]
\[\Rightarrow \left( 21.63+2 \right)\pi \text{ }c{{m}^{2}}\]
By substituting the values of \[\pi =\dfrac{22}{7}\], we get,
\[S=23.63\times \dfrac{22}{7}c{{m}^{2}}\]
\[S=74.26\text{ }c{{m}^{2}}\]
Hence, we get the total external surface area of the shuttlecock as \[74.26\text{ }c{{m}^{2}}\].
Note: Students are always advised to draw the diagram first in these types of questions. Also, students should properly do the calculations and take care while putting the decimal in numbers. In this question, some students make this mistake of calculating the total surface area instead of curved surface area, but as we can see that, we only need a curved surface area here to calculate the external area. So this mistake must be taken care of.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Difference Between Plant Cell and Animal Cell

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Who is eligible for RTE class 9 social science CBSE

Which places in India experience sunrise first and class 9 social science CBSE

What is pollution? How many types of pollution? Define it

Name 10 Living and Non living things class 9 biology CBSE




